Problemas de mecánica lagrangiana
Dos partículas de masa 
, unidas mediante un muelle de constante elástica 
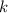y longitud natural despreciable, giran con velocidad angular constante 
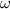con respecto a un eje vertical que pasa por el centro de masas del sistema. Las partículas se mueven sobre un plano horizontal sin rozamiento. Determine:
1.El Lagrangiano del sistema.
2.Las correspondientes ecuaciones de Lagrange.
3.La integral de Jacobi.
Considera un oscilador armónico multidimensional, dado por el potencial
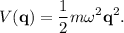
Encuentra el lagrangiano, los momentos conjugados y el hamiltoniano del sistema. Utiliza coordenadas rectilíneas.
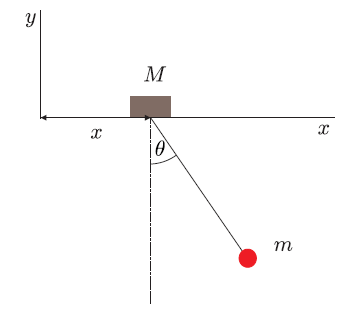
Considere el sistema formado por la masa 
que puede deslizar libremente sobre una recta horizontal, y unida mediante una varilla rígida y sin masa a M,pudiendo girar libremente en un plano vertical.
1.Obtenga la Lagrangiana de este sistema.
2.Determine las integrales primeras de movimiento.
3.Suponga ahora que se impone una velocidad constante 
a y discuta la existencia de integrales primeras.
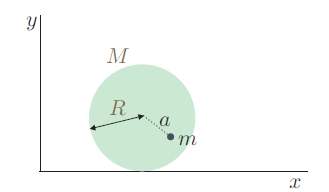
Un disco uniforme de masa y radio 
lleva adherida una masa a una distancia a de su centro. Si el disco puede rodar sin deslizar sobre un plano horizontal, determine la frecuencia de las pequeñas oscilaciones alrededor de la posición de equilibrio. El plano que contiene al disco es vertical.
Encontraremos primero las ecuaciones de movimiento con la formulación de Lagrange para luego imponer en ellas las condiciones de pequeñas oscilaciones y que éstas sean alrededor de la posición de equilibrio.
Coordenadas y velocidad de :
Debido a la ligadura de rodar sin deslizar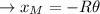 
, donde el menos proviene de suponer que la apartamos del equilibrio hacia la izquierda tal que la masa quede a la derecha de la vertical que pasa por el radio para concordar con la figura.
Así:
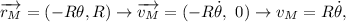
lo que era de esperar por la condición de rodadura, donde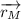 
es la posición del CM del disco de masa .
Coordenadas y velocidad de :
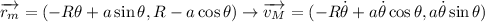
con lo que
Para las energías cinéticas:
tendrá energía cinética de traslación y de rotación. Si suponemos que es rígido:
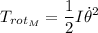
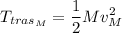
Calculemos el momento de inercia del disco: El tensor de inercia para una distribución continua de masa es:
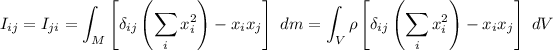
Como nos interesa el momento principal de inercia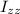 
que se corresponde al momento de inercia respecto a un eje perpendicular al disco que pase por su centro, nos queda la integral (si además consideramos que es una distribución continua superficial de masa cuya densidad superficial es constante):
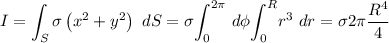
donde hemos hecho un cambio a coordenadas cilíndricas.
Si tenemos en cuenta que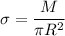 
de la definición de densidad superficial, queda:
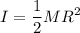
luego
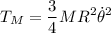
tendrá energía cinética de traslación únicamente dada por
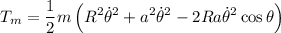
Con lo que
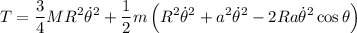
La energía potencial será
Para :
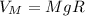
Para :
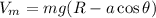
por lo que
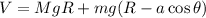
La Lagrangiana será:
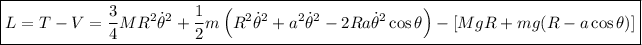
De las ecuaciones de Lagrange, para nuestra única coordenada generalizada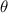 
nos queda:
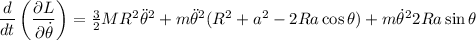
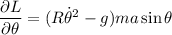
Con lo que
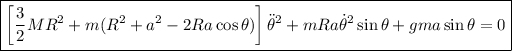
ahora imponemos
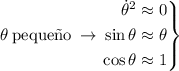
Luego nuestra ecuación de movimiento se reduce a
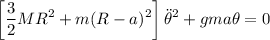
Lo cual es un M.A.S. de frecuencia angular:
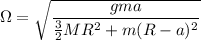
de donde como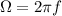 
;
Como nota, vemos que si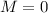 
(soporte sin masa) y 
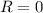queda la frecuencia de un M.A.S. hecho por 
comportándose como un péndulo de pequeña amplitud.
Tenemos una masa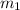 
unida a un muelle de constante recuperadora 
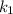, cuyo otro extremo esta fijado a un punto. Otra masa 
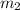está unida a la primera masa mediante otro muelle de constante 
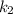. Todos los muelles cumplen la ley de Hooke. Ambas masas están obligadas a moverse en una única dirección.
1.Justifica cuantos grados de libertad tiene este sistema. Razona cuales son las coordenadas generalizadas más adecuadas para estudiarlo.
2.Escribe el lagrangiano del sistema.
3.Escribe el hamiltoniano del sistema.
4.Identifica las cantidades conservadas del sistema.
5.Obtén las ecuaciones del movimiento en el espacio de configuración (formulismo lagrangiano).
6.Desacopla y resuelve las ecuaciones del movimiento para el caso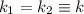 
y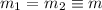 
. Aplica la solución general al caso en que las dos masas parten del reposo, la primera en el equilibrio y la segunda desplazada una distancia 
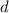de su posición de equilibrio.
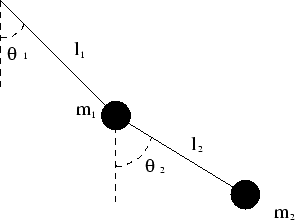
La masa 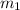de la figura siguiente esta unida a un punto fijo con una vara de longitud fija 
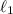, de forma que puede girar libremente respecto del punto fijo. De la misma forma, la masa 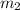esta unida a la anterior por otra vara rígida de longitud 
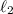que puede girar libremente, independientemente de la posición de la primera vara. Consideramos que las dos masas pueden moverse tan sólo dentro del plano del papel.
1.Justifica cuantos grados de libertad tiene este sistema. Escribe las ecuaciones que relacionan las posiciones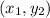 
y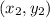 
con las coordenadas generalizadas más adecuadas para describir el sistema.
2.Escribe el lagrangiano del sistema.
3.Escribe los momentos conjugados.
4.Identifica las cantidades conservadas del sistema.
5.Obtén las ecuaciones del movimiento en el espacio de configuración (formulismo lagrangiano).
6.En la aproximación de ángulos muy pequeños, el péndulo simple se reduce a un oscilador armónico. Demuestra que, en esta misma aproximación, el péndulo doble se reduce al doble oscilador del problema anterior. ¿Cuál es la relación entre las coordenadas generalizadas de ambos sistemas?
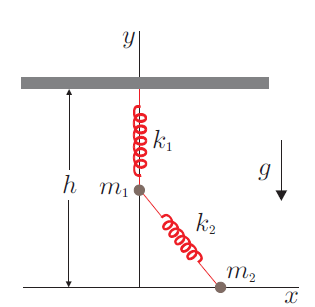
Considere el sistema de la figura, donde la masa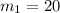 
kg está obligada a moverse verticalmente según el eje y, mientras que m
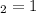kg está obligada a moverse según el eje x, ambas bajo la acción de dos muelles de constantes recuperadoras 
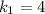N/m y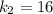 
N/m, además de la gravedad (Considere la longitud en reposo de los muelles nula).
1.Calcule la lagrangiana del sistema.
2.Obtenga las ecuaciones del movimiento para las masas.
3.Obtenga la solución general de las mismas y la posición de equilibrio.
4.Escriba la solución sabiendo que inicialmente se parte del reposo con 
m, 
m. Si 
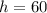m y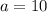 
m, determine la posición de las masas al cabo de 
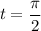segundos.
Una varilla de longitud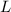 
se encuentra fija por un extremo a un eje vertical. La varilla gira con velocidad angular 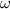alrededor de dicho eje. Determine el ángulo 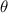que la varilla forma con el eje.
