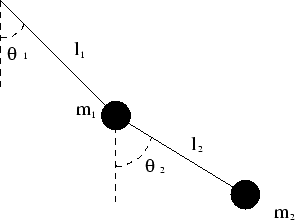
La masa 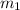de la figura siguiente esta unida a un punto fijo con una vara de longitud fija 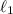, de forma que puede girar libremente respecto del punto fijo. De la misma forma, la masa 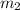esta unida a la anterior por otra vara rígida de longitud 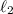que puede girar libremente, independientemente de la posición de la primera vara. Consideramos que las dos masas pueden moverse tan sólo dentro del plano del papel.

Figura 1. Péndulo doble

1.Justifica cuantos grados de libertad tiene este sistema. Escribe las ecuaciones que relacionan las posiciones 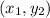y 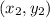con las coordenadas generalizadas más adecuadas para describir el sistema.

2.Escribe el lagrangiano del sistema.

3.Escribe los momentos conjugados.

4.Identifica las cantidades conservadas del sistema.

5.Obtén las ecuaciones del movimiento en el espacio de configuración (formulismo lagrangiano).

6.En la aproximación de ángulos muy pequeños, el péndulo simple se reduce a un oscilador armónico. Demuestra que, en esta misma aproximación, el péndulo doble se reduce al doble oscilador del problema anterior. ¿Cuál es la relación entre las coordenadas generalizadas de ambos sistemas?