Tenemos una masa 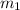unida a un muelle de constante recuperadora 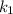, cuyo otro extremo esta fijado a un punto. Otra masa 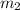está unida a la primera masa mediante otro muelle de constante 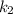. Todos los muelles cumplen la ley de Hooke. Ambas masas están obligadas a moverse en una única dirección.

1.Justifica cuantos grados de libertad tiene este sistema. Razona cuales son las coordenadas generalizadas más adecuadas para estudiarlo.

2.Escribe el lagrangiano del sistema.

3.Escribe el hamiltoniano del sistema.

4.Identifica las cantidades conservadas del sistema.

5.Obtén las ecuaciones del movimiento en el espacio de configuración (formulismo lagrangiano).

6.Desacopla y resuelve las ecuaciones del movimiento para el caso 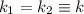y 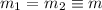. Aplica la solución general al caso en que las dos masas parten del reposo, la primera en el equilibrio y la segunda desplazada una distancia 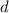de su posición de equilibrio.