Problemas de integración
Para resolver esta integral podemos aplicar el resultado del Teorema de Leibniz. Derivando respecto el parámetro:
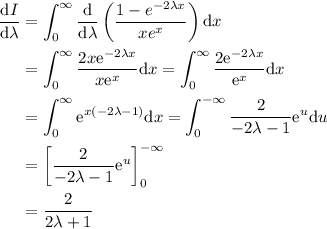
Durante la resolución hemos aplicado el cambio de variable 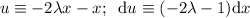 , al hacerlo, los nuevos límites de integración han sido, 0 para el inferior y
, al hacerlo, los nuevos límites de integración han sido, 0 para el inferior y 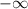 para el superior.
para el superior.
Ahora tenemos la siguiente ecuación diferencial de variables separadas:
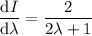
Integrando llegamos a:
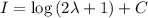
Para determinar el valor de la constante podemos ir a la integral y hacer 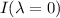 , vemos que el numerador se hace cero, con lo cual
, vemos que el numerador se hace cero, con lo cual 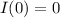 , por lo tanto
, por lo tanto
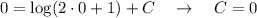
Finalmente
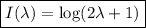
Sean las integrales
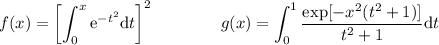
1.Demostrad que 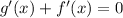 y que
y que 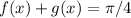
2.A continuación,teniendo en cuenta que 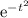 es una función con simetría par,utilizad este resultado para mostrar que
es una función con simetría par,utilizad este resultado para mostrar que
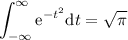
Sea la función 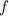 definida mediante
definida mediante
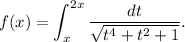
Estudiar las asíntotas y la monotonía de 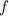 . Dibujar aproximadamente la gráfica de
. Dibujar aproximadamente la gráfica de 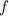 .
.

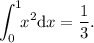

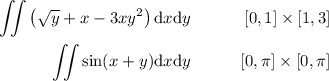
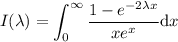
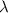 (siendo
(siendo 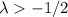 )
)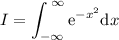
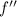 es continua y que
es continua y que 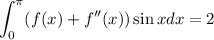 . Sabiendo que
. Sabiendo que 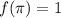 , calcule
, calcule 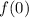 .
.