Problemas de Álgebra vectorial
Dados los vectores 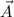 y
y 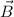 con origen en el punto común
con origen en el punto común 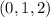 y extremos A(-1,2,3) y B(2,-1,1) respectivamente, calcular:
y extremos A(-1,2,3) y B(2,-1,1) respectivamente, calcular:
1.Producto escalar  .
.
2.Producto vectorial 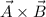 .
.
3.Producto vectorial  .
.
La velocidad de un móvil es 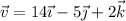 . Una fuerza
. Una fuerza 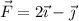 actúa sobre él. Calcula la componente de dicha fuerza en la dirección del movimiento y en la dirección perpendicular a él.
actúa sobre él. Calcula la componente de dicha fuerza en la dirección del movimiento y en la dirección perpendicular a él.
Dados los vectores 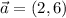 y
y 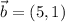 , calcula:
, calcula:
1.El producto escalar de ambos vectores.
2.La proyección de 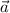 , sobre
, sobre 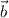
3.Las coordenadas de un vector unitario de la misma dirección que 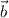
4.Un vector de la misma dirección que 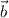 y cuyo módulo sea igual a la proyección de
y cuyo módulo sea igual a la proyección de 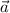 sobre
sobre 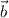 .
.
Dados dos vectores 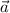 y
y 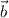 , obtener el vector proyección ortogonal de
, obtener el vector proyección ortogonal de 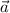 sobre
sobre 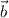 . Aplicarlo al caso en que [ERROR DE LaTeX. Error: 4 ] , [ERROR DE LaTeX. Error: 4 ] y
. Aplicarlo al caso en que [ERROR DE LaTeX. Error: 4 ] , [ERROR DE LaTeX. Error: 4 ] y 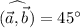 , obtener también la proyección ortogonal de
, obtener también la proyección ortogonal de 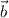 sobre
sobre 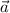 .
.
Se define la proyección de un vector 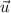 sobre otro
sobre otro 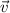 como
como 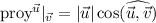 . Como conocemos el módulo de los vectores y el ángulo que forman sólo hemos de hacer uso de la definición de la proyección, ésta será el módulo del vector que nos piden y la dirección la del vector sobre el que se proyecta, en el primer caso tendremos que
. Como conocemos el módulo de los vectores y el ángulo que forman sólo hemos de hacer uso de la definición de la proyección, ésta será el módulo del vector que nos piden y la dirección la del vector sobre el que se proyecta, en el primer caso tendremos que
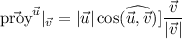
En los dos casos que nos han pedido, tendremos que
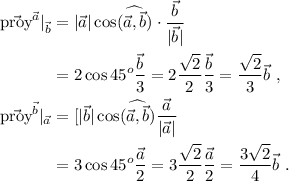
Halla el momento con respecto al punto P(0,-1,1) del vector unitario con origen en O(2,2,2) y que es paralelo al vector 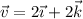 .
.


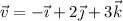 , halla otra de la misma dirección y sentido contrario, de módulo 3.
, halla otra de la misma dirección y sentido contrario, de módulo 3.