Problemas de leyes de newton en una dimensión
Si al aplicar una fuerza a un cuerpo aparece una reacción igual y de sentido contrario, ¿cómo es posible que lo ponga en movimiento?
Un trabajador debe lanzar un paquete de 5kg desde el suelo hasta una altura de 4m. Si el trabajador aplica al paquete una fuerza vertical constante desde el suelo hasta que encuentra a una altura de 1,5m, calcula:
1.el módulo de la fuerza mínima necesaria para que el paquete alcance los 4 m.
2.en estas condiciones, tiempo total empleado en subir el paquete.
Una persona está sobre una balanza dentro de un ascensor que sube con aceleración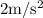 
(aceleración y velocidad del ascensor apuntan hacia arriba). Si la masa de la persona es 89kg, encontrar el peso (aparente) que marca la balanza en esta situación.
Tres bloques A, B y C (de masas 1, 2 y 3 kg, respectivamente) se encuentran sobre una superficie horizontal como se indica en la figura siguiente.
1.¿Qué fuerza hay que aplicarle a C para que los bloques adquieran una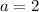 
m/s
?
2.Fuerza que ejerce A sobre B.
3.Fuerza que ejerce B sobre C.
4.Repetir el problema si suponemos que la fuerza se aplica sobre A (hacia la derecha).
El coeficiente de fricción estática entre el piso de un camión y una caja que descansa sobre el es de 0,30. La velocidad del camión es de 22.22m/s. ¿Cual es la distancia mínima de frenado del camión para que la caja no se deslice?
Un cuerpo de masa 2 kg desciende en caída libre. Toma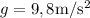 
.
1.¿Qué fuerza constante es necesario aplicarle en el instante en que su velocidad es de 20,4 m/s para detenerlo en 2 s?
2.¿Qué trabajo se realiza sobre el cuerpo desde que se aplica la fuerza hasta que se detiene?
Tenemos una jaula de 1kg de peso, y un pájaro en su interior que pesa 10g. Si el pájaro no se posa en la jaula, sino que permanece revoloteando, ¿cuánto pesará el conjunto de la jaula y el pájaro si la jaula es hermética? ¿y si es de barrotes?
Para despegar, dos planeadores se arrastran uno tras el otro mediante un avión de
transporte. La masa de cada planeador es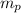 
y la fuerza con que se oponen al arrastre es
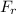. Los cables empleados para unir los tres aviones no deben someterse a tensiones
superiores a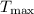 
. ¿Cuál es la aceleración máxima con que puede arrastrar los
planeadores sin que se rompan los cables? ¿Cuál es la longitud mínima de pista
requerida, si es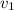 
la velocidad de despegue?
Suponemos gotas de lluvia que caen desde una cierta altura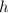 
. Si no hubiera fricción, calcular la velocidad con la que llega a tierra. Ahora suponemos que las gotas experimentan una fuerza de fricción 
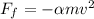. Calcular 
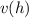y encontrar la velocidad límite. Para una aplicación realista supondremos los siguientes datos: 
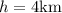y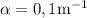 
.
Una cobra real de longitud L y masa m uniformemente distribuida reposa sobre el suelo. La cobra decide elevarse verticalmente. ¿Cuál será el valor de la fuerza media que ejerce el suelo sobre ella y hace que la cobra se eleve hacia arriba con una velocidad constante v? Despreciar todo tipo de rozamiento.
Un punto de masa 
se mueve por una trayectoria rectilínea bajo la acción de una fuerza proporcional al tiempo (el coeficiente de proporcionalidad es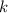 
). Además, el punto experimenta por parte del medio una resistencia viscosa por parte del aire proporcional a la velocidad (el coeficiente de proporcionalidad es 
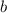). En el instante inicial la velocidad es igual a cero.
1.Encuentre la evolución de la velocidad respecto del tiempo en el caso en que no hay resistencia del aire (es decir, cuando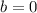 
).
2.Resuelva el problema en el caso general, con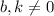 
.
3.Compruebe que el resultado del segundo apartado se reduce al del primero tomando el límite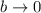 
.
Si no actúa la fricción viscosa, la segunda ley de Newton se convierte en la siguiente ecuación diferencial,
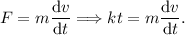
Esta es una ecuación diferencial separable, que se puede resolver con la manipulación formal de los diferenciales,
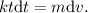
Finalmente, podemos integrar entre el momento inicial (en que el tiempo y la velocidad son ambos 0) y un instante genérico en que el tiempo es t y la velocidad v(t),
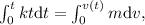
lo que nos da
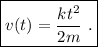
La aparición de la fuerza de fricción viscosa se traduce en un nuevo término en nuestra ecuación diferencial. Comoquiera que la fuerza de fricción siempre es opuesta al movimiento, entonces dicho término siempre tendrá signo opuesto a la velocidad. Por lo tanto, el término adicional tomará la forma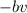 
. Con lo cual, la ecuación diferencial a resolver es
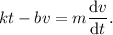
Ya no tenemos una ecuación separable. No obstante, no se trata de una ecuación mucho más difícil, ya que reorganizando los términos,
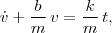
reconocemos una ecuación diferencial de primer grado lineal con coeficientes constantes y un término inhomogéneo. Recordad que el punto señala la derivación respecto del tiempo. La solución de este tipo de ecuaciones se puede hallar a partir de la solución general de la ecuación homogénea (es decir, retirando todos los términos que dependan de t de forma explícita) más una solución particular de la ecuación completa.
La ecuación homogénea es
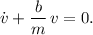
Esta ecuación puede resolverse por el método habitual de ensayar una solución del tipo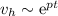 
, o bien dándonos cuenta de que esta sí es una ecuación separable. Mediante cualquiera de los métodos, el resultado es
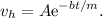
Para encontrar una solución particular a la ecuación (5) podemos inspirarnos en el hecho de que el término inhomogéneo es polinomial. En estos casos, conviene ensayar una solución también polinomial del mismo grado. Es decir, probamos una solución del estilo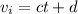 
. Una solución de este estilo arroja la siguiente ecuación,
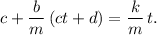
Dicha ecuación debe ser válida para cualquier instante de tiempo. Por lo tanto, los coeficientes de cada término del polinomio deben satisfacer la ecuación, lo cual nos permite obtener dos ecuaciones,
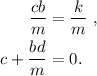
\end{aligned}
De la primera ecuación obtenemos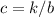 
. Substituyendo este resultado en la otra ecuación obtenemos
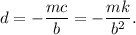
Por lo tanto, la solución particular es
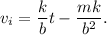
Juntando todas las piezas, la solución general de la ecuación competa (5) es
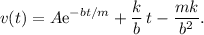
Esta solución está sometida a la condición inicial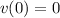 
, lo cual implica 
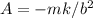. Con esto, el resultado final es
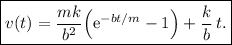
Este último apartado nos invita a analizar el comportamiento asintótico de la solución (13) cuando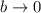 
. Vemos que una aplicación ingenua del límite no es muy prometedora, ya que 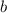aparece en el denominador de diversas fracciones. En estos casos, la forma más prometedora de proceder es realizar una expansión de Taylor. En nuestro caso, necesitamos la expansión de la exponencial,
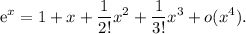
En nuestro caso tenemos
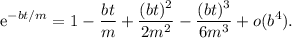
Insertando este resultado en (13) obtenemos
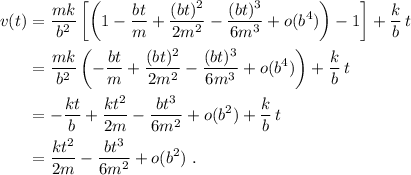
Tan sólo el primer término sobrevive cuando 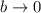, por lo que tenemos
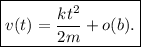
Efectivamente, el resultado es coherente con el que obtuvimos en (3). Nótese que hemos necesitado mantener los tres primeros términos del desarrollo de Taylor, ya que los dos primeros se anulaban en el resultado final. Si hubiéramos mantenido menos términos de los necesarios, hubiéramos obtenido cero como resultado final. Como norma general, si tras aplicar un desarrollo de Taylor nos sale cero, normalmente significa que debemos mantener más términos del desarrollo. En nuestro caso concreto, el hecho de que hubiera un coeficiente con una potencia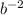 
era un claro indicador de que íbamos a necesitar expandir hasta, por lo menos, 
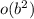. Por otra parte, nunca está de más mantener un término extra que será desechado al final (como hemos hecho esta vez).
La fuerza de rozamiento de un cuerpo con un medio fluido se suele modelizar con expresiones del tipo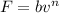 
, donde n = 1, 2, etc., y 
es la velocidad del cuerpo relativa al medio. Para ponerlo en práctica, imaginaremos un velero de masa que se mueve impulsado por un viento de de velocidad 
(respecto al mar). La fuerza de impulsión se puede considerar como el rozamiento con el aire, con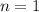 
y constante de proporcionalidad 
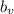. Consideraremos también la existencia de el rozamiento con el agua, con 
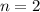y constante 
.
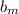1.Escribir la expresión de todas las fuerzas que intervienen en el movimiento del velero en función de la velocidad del mismo, siguiendo un convenio de signos coherente.
2.¿Cuál es la velocidad de crucero del velero?
3.Encuentra la velocidad del velero en función del tiempo, suponiendo que comienza parado.
4.Encuentra la posición del velero en función del tiempo, suponiendo que comienza en el origen.
5.Utilizando la solución analítica, verifica que la velocidad de crucero es la calculada en el anterior apartado.
Sabiendo que el momento lineal de una onda electro magnética és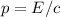 
donde E es la energía de esta onda y c la velocidad de la luz, calcula la fuerza que ejerce una onda con un flujo de energía de 
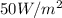sobre una cartulina negra de 3cm de lado, que la absorbe completamente
Considerando una fuerza constante que actúa tan sólo entre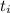 
y 
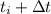, con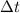 
mucho menor que cualquier otra escala de tiempos del problema (con lo cual podemos quedarnos, en cada momento, con el primer orden) obtén la función de Green del oscilador armónico amortiguado, con frecuencia natural 
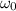y coeficiente de rozamiento 
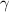. Considerar los tres casos posibles:
1.oscilador sobreamortiguado,
2.amortiguamiento crítico y
3.oscilador infraamortiguado.
Considera un oscilador armónico simple de frecuencia natural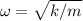 
, el cual se mueve sobre la superficie del suelo, lo que produce una fuerza de rozamiento constante, de valor 
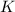. El oscilador comienza, en reposo, separado una distancia 
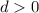de la posición donde la fuerza de recuperación es nula. Calcula cual será la evolución ulterior del oscilador. Considera iguales las fuerzas de fricción estática y dinámica.
