Problemas de leyes de newton en una dimensión
Nivel: Primer ciclo
Para despegar, dos planeadores se arrastran uno tras el otro mediante un avión de
transporte. La masa de cada planeador es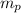 
y la fuerza con que se oponen al arrastre es
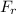. Los cables empleados para unir los tres aviones no deben someterse a tensiones
superiores a 
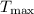. ¿Cuál es la aceleración máxima con que puede arrastrar los
planeadores sin que se rompan los cables? ¿Cuál es la longitud mínima de pista
requerida, si es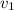 
la velocidad de despegue?
Suponemos gotas de lluvia que caen desde una cierta altura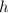 
. Si no hubiera fricción, calcular la velocidad con la que llega a tierra. Ahora suponemos que las gotas experimentan una fuerza de fricción 
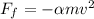. Calcular 
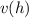y encontrar la velocidad límite. Para una aplicación realista supondremos los siguientes datos: 
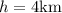y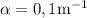 
.
En primer lugar realizaremos el caso en el que no hay fricción. Para ello utilizaremos la ley de la conservación de la energía, es decir, la energía mecánica inicial es igual a la energía mecánica final
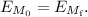
Como la velocidad inicial la supondremos que es nula, la T será 0, eso quiere decir que en el instante inicial las gotas están paradas. Lo mismo con la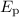 
que obtendrá tambien el valor 0, ya que la altura final la consideraremos 0. Quedando la siguiente ecuación
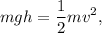
aislando la velocidad final de manera que nos queda
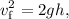
de manera que sustituyendo nos dará
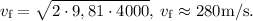
Para el siguiente caso, en que hay fuerza de fricción, aplicamos la segunda ley de Newton, considerando que la únicas fuerzas que actúan en la gota son, su peso y la fuerza de fricción
para ahora hallar 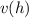utilizaremos la regla de la cadena
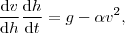
teniendo en cuenta que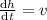 
, y desarrollando los siguientes pasos para la integración
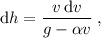
ahora con sus correspondientes limites de integración
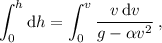
sabiendo que es una integral inmediata del tipo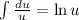 
, nos queda
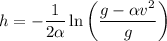
y aislando 
en la ecuación de la manera siguiente, obtenemos la velocidad en función de la altura
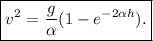
Para encontrar ahora la velocidad límite de la gota, se puede plantear de varias maneras: sabemos que cuando la velocidad es máxima la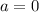 
, también razonando que cuando el peso se iguala con la fuerza de fricción, la velocidad es constante 
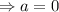; de manera que podremos considerar el caso en que la altura tiende a 0
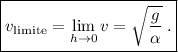
Una cobra real de longitud L y masa m uniformemente distribuida reposa sobre el suelo. La cobra decide elevarse verticalmente. ¿Cuál será el valor de la fuerza media que ejerce el suelo sobre ella y hace que la cobra se eleve hacia arriba con una velocidad constante v? Despreciar todo tipo de rozamiento.
Un punto de masa 
se mueve por una trayectoria rectilínea bajo la acción de una fuerza proporcional al tiempo (el coeficiente de proporcionalidad es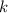 
). Además, el punto experimenta por parte del medio una resistencia viscosa por parte del aire proporcional a la velocidad (el coeficiente de proporcionalidad es 
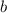). En el instante inicial la velocidad es igual a cero.
1.Encuentre la evolución de la velocidad respecto del tiempo en el caso en que no hay resistencia del aire (es decir, cuando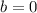 
).
2.Resuelva el problema en el caso general, con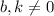 
.
3.Compruebe que el resultado del segundo apartado se reduce al del primero tomando el límite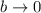 
.
La fuerza de rozamiento de un cuerpo con un medio fluido se suele modelizar con expresiones del tipo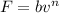 
, donde n = 1, 2, etc., y es la velocidad del cuerpo relativa al medio. Para ponerlo en práctica, imaginaremos un velero de masa que se mueve impulsado por un viento de de velocidad 
(respecto al mar). La fuerza de impulsión se puede considerar como el rozamiento con el aire, con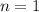 
y constante de proporcionalidad 
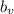. Consideraremos también la existencia de el rozamiento con el agua, con 
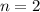y constante 
.
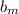1.Escribir la expresión de todas las fuerzas que intervienen en el movimiento del velero en función de la velocidad del mismo, siguiendo un convenio de signos coherente.
2.¿Cuál es la velocidad de crucero del velero?
3.Encuentra la velocidad del velero en función del tiempo, suponiendo que comienza parado.
4.Encuentra la posición del velero en función del tiempo, suponiendo que comienza en el origen.
5.Utilizando la solución analítica, verifica que la velocidad de crucero es la calculada en el anterior apartado.
Sabiendo que el momento lineal de una onda electro magnética és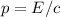 
donde E es la energía de esta onda y c la velocidad de la luz, calcula la fuerza que ejerce una onda con un flujo de energía de 
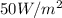sobre una cartulina negra de 3cm de lado, que la absorbe completamente
Considerando una fuerza constante que actúa tan sólo entre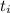 
y 
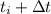, con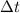 
mucho menor que cualquier otra escala de tiempos del problema (con lo cual podemos quedarnos, en cada momento, con el primer orden) obtén la función de Green del oscilador armónico amortiguado, con frecuencia natural 
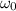y coeficiente de rozamiento 
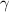. Considerar los tres casos posibles:
1.oscilador sobreamortiguado,
2.amortiguamiento crítico y
3.oscilador infraamortiguado.
Considera un oscilador armónico simple de frecuencia natural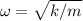 
, el cual se mueve sobre la superficie del suelo, lo que produce una fuerza de rozamiento constante, de valor 
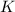. El oscilador comienza, en reposo, separado una distancia 
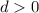de la posición donde la fuerza de recuperación es nula. Calcula cual será la evolución ulterior del oscilador. Considera iguales las fuerzas de fricción estática y dinámica.
