Problemas de oscilador armónico simple
Nivel: Secundaria
El desplazamiento de una partícula viene dado por
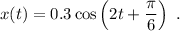
(x en metros y t en segundos).
1.Determinar la frecuencia, el periodo, la amplitud, la pulsación y la fase inicial.
2.¿Dónde se encuentra la partícula en t = 1s?
3.Calcula la velocidad y la aceleración en un instante cualquiera, t.
4.Calcula la posición y velocidad inicial.
Un resorte metálico del que pende una masa m, si se estira ligeramente, comienza a oscilar al dejarlo en libertad. Si cambiamos la masa por otra mayor o menor, ¿se verá afectado el período?, ¿por qué?
Una balanza de resorte, con una constante elástica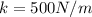 
, cuelga verticalmente y una bandeja de 
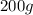se suspende de su extremo inferior. Un carnicero suelta un filete de 
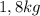sobre la bandeja desde una altura de 
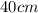, después de lo cual la bandeja oscila con movimiento armónico simple. Calcular:
1.la amplitud,
2.el periodo T,
3.la energía potencial del resorte justo en la posición de equilibrio.
Dibuje el esquema experimental.
Primero tenemos que determinar la velocidad inicial con la que empieza a oscilar la bandeja lo que se hace por conservación de la energía:
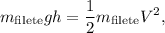
luego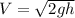 
, pero al impactar con la bandeja por la conservación de la cantidad de movimiento se tendrá que:
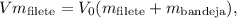
entonces la badeja empezará a oscilar con una velocidad de:
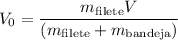
Sabemos que la amplitud de una oscilación simple esta dada por:
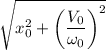
Donde:
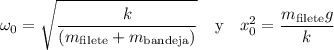
ya que la posición de equilibrio de la oscilación sucede cuando la masa total es igual a la fuerza elástica, y como ya estaba deformado el resorte por acción de la balanza, la posición inicial resulta de restar la deformación total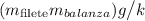 
menos la deformación ocasionada por la balanza 
.
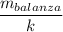Luego de reemplazar los datos se tiene que: 
El periódo será:
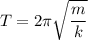
reemplazando se tiene que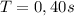 
.
Como la energía potencial del resorte en la posición de equilibrio para este caso solo depende de la elongación del resorte y de la distancia que baja por acción de la masa; esta estará dada por: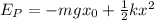 
, entonces:
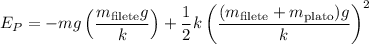
reemplazando: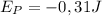 
.
Un hilo elástico de constante elástica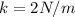 
de área transversal igual a 
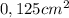y de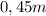 
de longitud natural, sostiene verticalmente desde un punto fijo un bloque de 
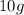de masa formando un péndulo simple. ¿Cuál es el periodo T de las oscilaciones de este péndulo?
1.En la tierra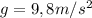 
.
2.En la luna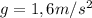 
.
Dibuje el esquema en cada caso. Suponga en todo momento que durante las oscilaciones la variación de la longitud del hilo es despreciable.
