Problemas de oscilador armónico simple
Nivel: Secundaria
El desplazamiento de una partícula viene dado por
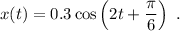
(x en metros y t en segundos).
1.Determinar la frecuencia, el periodo, la amplitud, la pulsación y la fase inicial.
2.¿Dónde se encuentra la partícula en t = 1s?
3.Calcula la velocidad y la aceleración en un instante cualquiera, t.
4.Calcula la posición y velocidad inicial.
Observamos que se trata de un movimiento armónico simple, cuya ecuación general viene dada por
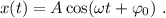
Comparando directamente con la expresión que nos da el enunciado vemos que
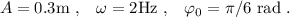
La frecuencia se obtiene a partir de la pulsación,
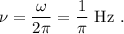
Por último, el periodo se calcula como la inversa de la frecuencia,
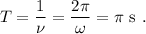
Para saber dónde se encuentra la partícula en el instante t = 1s es suficiente substituir en la ecuación del movimiento,
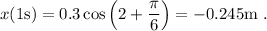
La velocidad y la aceleración se pueden obtener de la posición derivando respecto del tiempo (una vez para obtener la velocidad, dos para la aceleración). O bien, substituyendo los datos del apartado 1 si no hemos aprendido esta técnica todavía. En cualquier caso, el resultado es
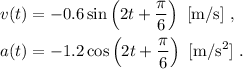
En este caso, únicamente tenemos que substituir t = 0 en las expresiones adecuadas,
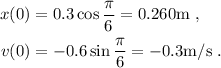
Un resorte metálico del que pende una masa m, si se estira ligeramente, comienza a oscilar al dejarlo en libertad. Si cambiamos la masa por otra mayor o menor, ¿se verá afectado el período?, ¿por qué?
Una balanza de resorte, con una constante elástica 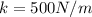 , cuelga verticalmente y una bandeja de
, cuelga verticalmente y una bandeja de 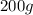 se suspende de su extremo inferior. Un carnicero suelta un filete de
se suspende de su extremo inferior. Un carnicero suelta un filete de 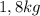 sobre la bandeja desde una altura de
sobre la bandeja desde una altura de 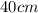 , después de lo cual la bandeja oscila con movimiento armónico simple. Calcular:
, después de lo cual la bandeja oscila con movimiento armónico simple. Calcular:
1.la amplitud,
2.el periodo T,
3.la energía potencial del resorte justo en la posición de equilibrio.
Dibuje el esquema experimental.
Un hilo elástico de constante elástica 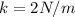 de área transversal igual a
de área transversal igual a 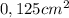 y de
y de 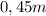 de longitud natural, sostiene verticalmente desde un punto fijo un bloque de
de longitud natural, sostiene verticalmente desde un punto fijo un bloque de 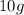 de masa formando un péndulo simple. ¿Cuál es el periodo T de las oscilaciones de este péndulo?
de masa formando un péndulo simple. ¿Cuál es el periodo T de las oscilaciones de este péndulo?
1.En la tierra 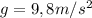 .
.
2.En la luna 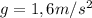 .
.
Dibuje el esquema en cada caso. Suponga en todo momento que durante las oscilaciones la variación de la longitud del hilo es despreciable.


