Problemas de integración por residuos

Vemos que la función a integrar es par, por lo que podemos extender la región de integración a todos los reales. Por lo tanto

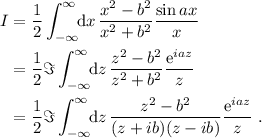
(1)

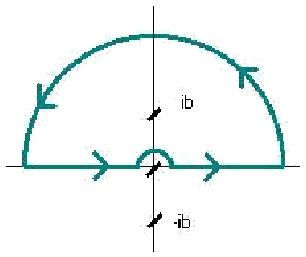
Como el integrando tiende a cero cuando 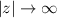, podemos extender el circuito de integración para incluir todo el semiplano complejo superior, esquivando el polo en z=0 por encima, tal y como mostramos en la figura 1.

Figura 1. Circuito de integración

Por lo tanto, nuestra integral original será igual a la contribución del polo en 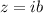, menos la integral en el rizo que se hace para evitar el polo en el origen:

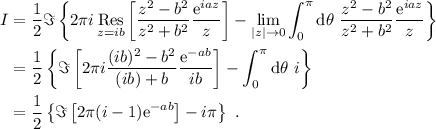
(2)

Por lo tanto,

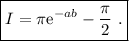
(3)
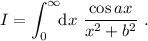
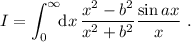
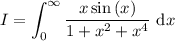
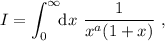
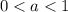