Problemas de inducción matemática
2
Suma de enteros
Nivel
Secundaria
Dificultad
5
Utiliza el principio de inducción para demostrar que la suma de los primeros N números enteros es 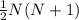 . Es decir,
. Es decir,
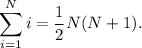
(1)
Solución disponible
Cat_in_a_box
3
Nivel
Primer ciclo
Dificultad
3
Solución disponible
pod
6
Demostración por inducción
Nivel
Primer ciclo
Dificultad
5
8
Nivel
Primer ciclo
Dificultad
7
Solución disponible
pod
9
Binomio de Newton
Nivel
Primer ciclo
Dificultad
7
Solución disponible
arreldepi
10
Nivel
Primer ciclo
Dificultad
9
Solución disponible
pod

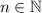 , se cumple
, se cumple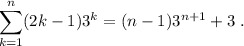

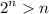 .
.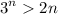 .
.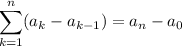 .
.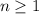
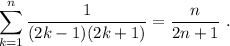
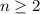 , se cumple
, se cumple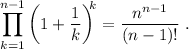
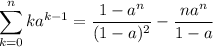
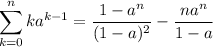
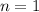
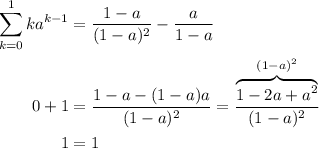

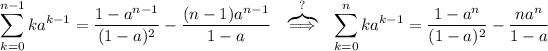
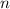 ).
).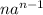 en ambos lados de la igualdad, es decir:
en ambos lados de la igualdad, es decir: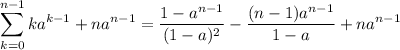
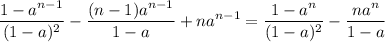
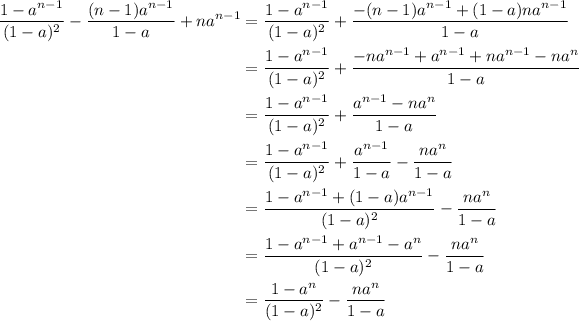
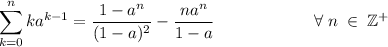
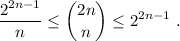
 , terminan en seis.
, terminan en seis.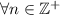 se cumple:
se cumple: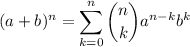
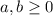 demostrar que para todo
demostrar que para todo 
