Problemas de física de fluidos
Nivel: Primer ciclo
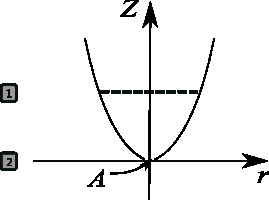
La clepsidra es un recipiente con simetría de revolución en la cual se coloca agua y posee un agujero pequeño en la parte inferior. Al ir vaciándose el agua la altura de esta indica el tiempo que transcurre. ¿Cuál debe de ser la forma de la curva generatriz para que la altura del agua sea lineal con el tiempo?
La idea a seguir es tratar de encontrar una ecuación de la forma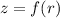 
.
Para ello haré uso de la siguiente figura:
Teniendo en cuenta el diagrama y los niveles de referencia 
y 
se aplica la ecuación de Bernoulli:
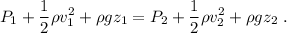
Donde:
, 
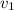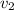: velocidad del fluido en cada nivel.
, 
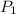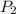: presiones en cada nivel del fluido.
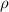: densidad del fluido.
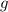: gravedad.
, 
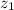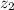: posiciones de los niveles 1 y 2 con respecto al nivel de referencia.
Ahora si tomamos como nivel de referencia a (
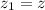y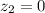 
), y teniendo en cuenta que la presión en ambos niveles es la presión atmosférica 
(
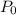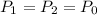) por estar abiertos al exterior, se tiene que:
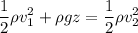
Además teniendo en cuenta la ecuación de continuidad:
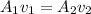
Y considerando que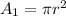 
se tiene de (2) y (3) que:
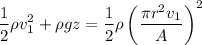
Luego despejando 
se tiene que:
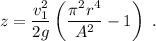
Que es lo que se quería encontrar. Si el agujero de salida es circular con radio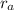 
, entonces 
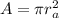, y por tanto
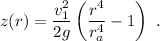
Para terminar, podemos utilizar cualquier software matemático para representar la clepsidra:
Un contenedor semiesférico de radio 
se llena con agua. La parte superior está abierta a la presión atmosférica. En la parte inferior existe un tapón abierto de radio mucho menor que . Halle el tiempo total necesario para vaciar el contenedor. Supóngase que el flujo es ideal.
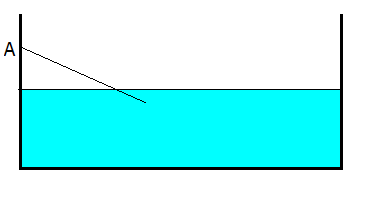
Una barra delgada y homogénea, de longitud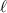 
y de densidad volumétrica de masa 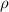, se encuentra sujeta por un extremo de un punto A, mientras que el otro extremo está sumergido en un líquido de densidad 
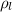. La barra puede moverse libremente alrededor de un eje perpendicular al plano de la figura y que pasa por A. ¿Qué porcentaje de longitud de la barra se halla sumergida, en la posición de equilibrio estable?
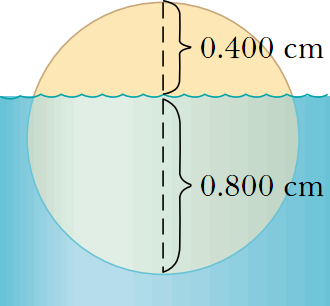
Una bola sólida y homogénea de diámetro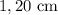 
está sumergida parcialmente en agua tal y como se muestra en la figura, y está en equilibrio. Determine su densidad.
Una bomba hidráulica de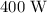 
de potencia útil es capaz de extraer el líquido contenido en un depósito con forma semiesférica en 
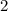minutos. Determinar la densidad del líquido sabiendo que el radio de la semiesfera es de 
.
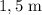Problema propuesto en examen de oposiciones a profesor de secundaria, especialidad Física y Química. Castilla-La Mancha, 2002.
