Problemas de geometría lineal y espacio afín
Nivel: Secundaria
1
Nivel
Secundaria
Dificultad
3
Solución disponible
Ghiret
2
Nivel
Secundaria
Dificultad
4
Solución disponible
Ghiret
3
Nivel
Secundaria
Dificultad
4
Solución disponible
Ghiret
4
Nivel
Secundaria
Dificultad
4
2 soluciones disponibles
pod
Ghiret
5
Nivel
Secundaria
Dificultad
5
Dados los planos
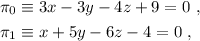
(1)
hallar la ecuación de la recta 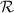 que pasa por el punto
que pasa por el punto  y es paralela a los dos planos.
y es paralela a los dos planos.
Solución disponible
Ghiret
6
Nivel
Secundaria
Dificultad
6
2 soluciones disponibles
pod
Llamaremos R a la recta perpendicular al plano 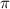 que pasa por el punto A. De la ecuación del plano
que pasa por el punto A. De la ecuación del plano 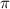 , sabemos que su vector perpendicular es (2, -1, -1), por lo que la recta R se puede escribir como
, sabemos que su vector perpendicular es (2, -1, -1), por lo que la recta R se puede escribir como
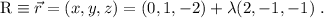
(1)
El punto de intersección entre la recta R y el plano 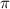 , que llamaremos
, que llamaremos  , se obtiene substituyendo los valores de
, se obtiene substituyendo los valores de  ,
, 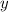 y
y  en la ecuación del plano:
en la ecuación del plano:
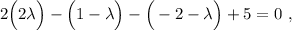
(2)
simplificando,
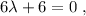
(3)
con lo que el punto de intersección se encuentra en 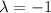 . Substituyendo en (1), tenemos
. Substituyendo en (1), tenemos
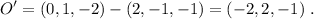
(4)
El vector que une los puntos O' y A se obtiene simplemente restando,
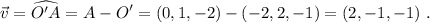
(5)
Por simetría, el vector que une el punto  con
con 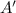 será
será 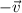 . Por tanto,
. Por tanto,
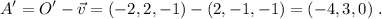
(6)
Ghiret
7
Nivel
Secundaria
Dificultad
8
2 soluciones disponibles
pod
Ghiret

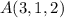 y es perpendicular a la recta
y es perpendicular a la recta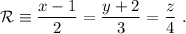

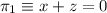 y
y 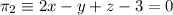 .
.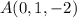 respecto del plano
respecto del plano 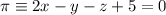 .
.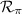 , proyección de la recta
, proyección de la recta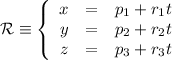
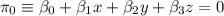 .
.