Problemas de dinámica de la rotación
Dada una fuerza de módulo 3N, aplicada en el punto (1,3,1) y tal que forma ángulos de 30º y 60º con los ejes X e Y, respectivamente. Halla su momento con respecto al punto (5,2,1).
Un cuerpo de 500g gira sobre una superficie horizontal sin rozamiento, atado por una cuerda de 80cm de longitud a una punta. Calcula la fuerza que soporta la cuerda cuando el cuerpo gira a 60rpm.
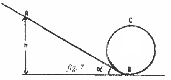
Un carro de 1T avanza horizontalmente y sin rozamiento sobre un carril con una velocidad inicial de 10m/s en el punto A, según expresa la figura. A continuación entra en un lazo vertical de 4m de radio.
Calcular:
1.La fuerza que ejerce el carril sobre el carro al pasar por el punto B (a media altura).
2.Velocidad mínima necesaria en A para que el carro alcance el punto C (cima del lazo) sin despegarse del carril.
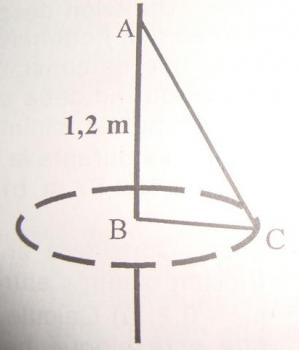
Un cuerpo de 50g colgado de un hilo de 1,2m de longitud describe una circunferencia de 0,5m de radio con velocidad constante. Calcula:
1.tensión del hilo.
2.velocidad de giro.
3.tiempo que tarda en dar una vuelta.
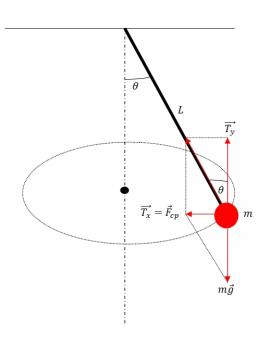
En primer lugar, observemos las fuerzas que actúan sobre el cuerpo que describe la circunferencia:
Sea 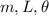 la masa del cuerpo, la longitud del hilo y el ángulo que circunscribe con la vertical. Se desea calcular la tensión que soporta la cuerda, así como el valor constante de la velocidad y el período.
la masa del cuerpo, la longitud del hilo y el ángulo que circunscribe con la vertical. Se desea calcular la tensión que soporta la cuerda, así como el valor constante de la velocidad y el período.
Como se dice en el enunciado, el cuerpo describe una circunferencia, en un plano horizontal, por lo que sólo actúa la fuerza centrípeta. Ahora bien, es obvio que ''actúan'' otras fuerzas,como son el peso y la tensión del hilo, con lo cual, la fuerza centrípeta será la resultante de ambas, que de forma vectorial es:
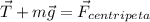
Descomponiendo la tensión en sus componentes horizontal y vertical, la igualdad vectorial anterior se traduce en:
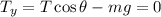
En lo que respecta a la dirección vertical. Observamos que en esta dirección la resultante es cero, lo cual explica la ausencia de movimiento del cuerpo en dicha dirección.
Por otro lado, en la dirección horizontal, tenemos que: 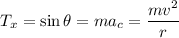
Concluimos que la componente 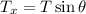 es la fuerza centrípeta que hace que el cuerpo describa la circunferencia con una velocidad constante.
es la fuerza centrípeta que hace que el cuerpo describa la circunferencia con una velocidad constante.
Pues bien, de la condición de equilibrio en la dirección vertical, se deduce que la tensión del hilo es igual a:
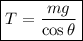
Ahora bien, ¿cuál es el ángulo 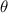 ? Como se observa en el diagrama, podemos deducir que el ángulo es:
? Como se observa en el diagrama, podemos deducir que el ángulo es:
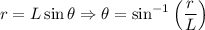
Siendo  el radio de la circunferencia que describe. Por tanto, podemos calcular la tensión del hilo:
el radio de la circunferencia que describe. Por tanto, podemos calcular la tensión del hilo:
[ERROR DE LaTeX. Error: 4 ]
Es posible calcular la velocidad, bien sustituyendo el valor obtenido de la tensión en la expresión de la descomposición de la tensión en la dirección vertical, o dividiendo miembro a miembro ambas expresiones:
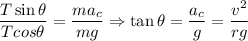
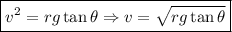
En nuestro caso:

Por último, deseamos calcular el período. Como la velocidad es constante, podemos expresarla como en un movimiento uniforme, es decir:
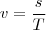
Donde  y
y 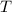 es el espacio recorrido, en este caso la longitud de la circunferencia,
es el espacio recorrido, en este caso la longitud de la circunferencia, 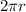 y el período de revolución, es decir, el tiempo que tarda en dar una vuelta completa. Por tanto:
y el período de revolución, es decir, el tiempo que tarda en dar una vuelta completa. Por tanto:
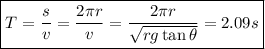
Una masa 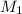 está atada en un extremo de una cuerda de longitud
está atada en un extremo de una cuerda de longitud 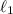 fija por el otro extremo, una segunda masa
fija por el otro extremo, una segunda masa 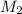 va unidad a la primera mediante otra cuerda de longitud
va unidad a la primera mediante otra cuerda de longitud 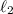 . Ambas se mueven sobre una superficie lisa horizontal con un movimiento circular de periodo
. Ambas se mueven sobre una superficie lisa horizontal con un movimiento circular de periodo 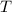 . Determinar la tensión en cada cuerda.
. Determinar la tensión en cada cuerda.
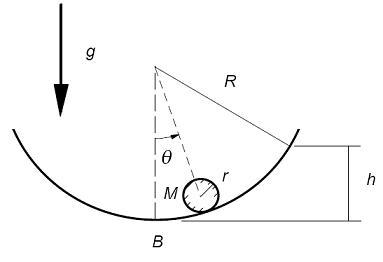
En la cima de una gran esfera fija de radio  se sitúa una pequeña canica maciza, también esférica, de radio
se sitúa una pequeña canica maciza, también esférica, de radio  y masa
y masa  . La canica parte del reposo y cae por la superficie de la esfera mayor sin deslizar. Calcula:
. La canica parte del reposo y cae por la superficie de la esfera mayor sin deslizar. Calcula:
1.La velocidad de la canica en función del ángulo con la vertical.
2.El ángulo que forma con la vertical en el momento en que deja de estar en contacto con la superficie.
3.La fuerza de fricción en función del ángulo
Un disco uniforme de masa  , radio
, radio  y espesor
y espesor 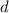 rueda sin resbalar sobre una superficie esférica de radio
rueda sin resbalar sobre una superficie esférica de radio  como se muestra en la figura. El movimiento es plano.
como se muestra en la figura. El movimiento es plano.
1.Encontrar el tiempo para el cuál el radio vector que une el centro del hemisferio esférico con el centro del disco barre un ángulo 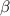 .
.
2.Encontrar el periodo para el caso en que 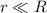 .
.
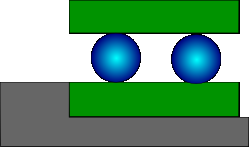
Consideramos el sistema de la figura 1.
El bloque inferior se mueve sobre raíles, con rozamiento despreciable. El sistema de los dos bloques y las dos ruedas se mueven hacia la izquierda de forma solidaria con velocidad constante 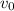 . En un instante dado, el bloque inferior colisiona con un escalón, de forma que se frena completamente de golpe. Ambos bloques están hechos del mismo material, y son lo suficientemente largos. La masa del bloque superior es
. En un instante dado, el bloque inferior colisiona con un escalón, de forma que se frena completamente de golpe. Ambos bloques están hechos del mismo material, y son lo suficientemente largos. La masa del bloque superior es  , y la de las ruedas
, y la de las ruedas 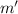 . Todos los cuerpos son homogéneos.
. Todos los cuerpos son homogéneos.
1.¿Qué condición debe cumplir el coeficiente de rozamiento entre los bloques y las ruedas para que el bloque superior no deslice sobre ellas?
2.Calcula la velocidad final de cada elemento del sistema.
3.Calcula la variación de energía cinética de cada elemento del sistema.
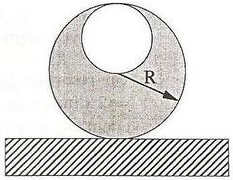
Considere un cilindro de radio  y densidad
y densidad 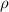 con una perforación cilíndrica de radio
con una perforación cilíndrica de radio 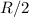 , tal como se muestra en la figura. El cilindro rueda sin resbalar sobre una superficie horizontal realizando pequeñas oscilaciones en torno a su posición de equilibrio. Encuentre el periodo de las oscilaciones.
, tal como se muestra en la figura. El cilindro rueda sin resbalar sobre una superficie horizontal realizando pequeñas oscilaciones en torno a su posición de equilibrio. Encuentre el periodo de las oscilaciones.


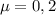 ). La inclinación del plano es de
). La inclinación del plano es de 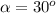 .
.