Problemas de dinámica de la rotación
Dada una fuerza de módulo 3N, aplicada en el punto (1,3,1) y tal que forma ángulos de 30º y 60º con los ejes X e Y, respectivamente. Halla su momento con respecto al punto (5,2,1).
Un cuerpo de 500g gira sobre una superficie horizontal sin rozamiento, atado por una cuerda de 80cm de longitud a una punta. Calcula la fuerza que soporta la cuerda cuando el cuerpo gira a 60rpm.
Un carro de 1T avanza horizontalmente y sin rozamiento sobre un carril con una velocidad inicial de 10m/s en el punto A, según expresa la figura. A continuación entra en un lazo vertical de 4m de radio.
Calcular:
1.La fuerza que ejerce el carril sobre el carro al pasar por el punto B (a media altura).
2.Velocidad mínima necesaria en A para que el carro alcance el punto C (cima del lazo) sin despegarse del carril.
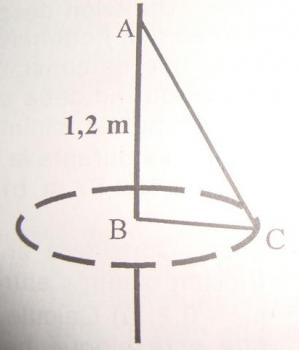
Un cuerpo de 50g colgado de un hilo de 1,2m de longitud describe una circunferencia de 0,5m de radio con velocidad constante. Calcula:
1.tensión del hilo.
2.velocidad de giro.
3.tiempo que tarda en dar una vuelta.
Una masa 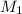 está atada en un extremo de una cuerda de longitud
está atada en un extremo de una cuerda de longitud 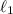 fija por el otro extremo, una segunda masa
fija por el otro extremo, una segunda masa 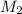 va unidad a la primera mediante otra cuerda de longitud
va unidad a la primera mediante otra cuerda de longitud 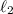 . Ambas se mueven sobre una superficie lisa horizontal con un movimiento circular de periodo
. Ambas se mueven sobre una superficie lisa horizontal con un movimiento circular de periodo 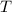 . Determinar la tensión en cada cuerda.
. Determinar la tensión en cada cuerda.
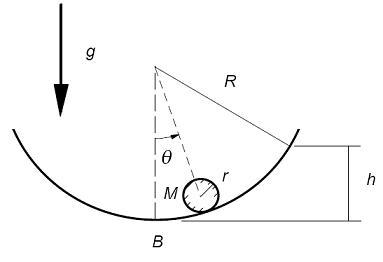
En la cima de una gran esfera fija de radio  se sitúa una pequeña canica maciza, también esférica, de radio
se sitúa una pequeña canica maciza, también esférica, de radio  y masa
y masa  . La canica parte del reposo y cae por la superficie de la esfera mayor sin deslizar. Calcula:
. La canica parte del reposo y cae por la superficie de la esfera mayor sin deslizar. Calcula:
1.La velocidad de la canica en función del ángulo con la vertical.
2.El ángulo que forma con la vertical en el momento en que deja de estar en contacto con la superficie.
3.La fuerza de fricción en función del ángulo
Un disco uniforme de masa  , radio
, radio  y espesor
y espesor 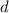 rueda sin resbalar sobre una superficie esférica de radio
rueda sin resbalar sobre una superficie esférica de radio  como se muestra en la figura. El movimiento es plano.
como se muestra en la figura. El movimiento es plano.
1.Encontrar el tiempo para el cuál el radio vector que une el centro del hemisferio esférico con el centro del disco barre un ángulo 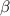 .
.
2.Encontrar el periodo para el caso en que 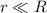 .
.
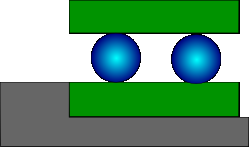
Consideramos el sistema de la figura 1.
El bloque inferior se mueve sobre raíles, con rozamiento despreciable. El sistema de los dos bloques y las dos ruedas se mueven hacia la izquierda de forma solidaria con velocidad constante 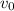 . En un instante dado, el bloque inferior colisiona con un escalón, de forma que se frena completamente de golpe. Ambos bloques están hechos del mismo material, y son lo suficientemente largos. La masa del bloque superior es
. En un instante dado, el bloque inferior colisiona con un escalón, de forma que se frena completamente de golpe. Ambos bloques están hechos del mismo material, y son lo suficientemente largos. La masa del bloque superior es  , y la de las ruedas
, y la de las ruedas 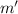 . Todos los cuerpos son homogéneos.
. Todos los cuerpos son homogéneos.
1.¿Qué condición debe cumplir el coeficiente de rozamiento entre los bloques y las ruedas para que el bloque superior no deslice sobre ellas?
2.Calcula la velocidad final de cada elemento del sistema.
3.Calcula la variación de energía cinética de cada elemento del sistema.
Tras la colisión con el escalón, el bloque inferior queda completamente parado, pero las ruedas y el bloque superior siguen moviéndose a la misma velocidad, inicialmente. Por lo tanto, entre las ruedas y el bloque inferior aparecerá una fuerza de rozamiento dinámico, 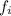 , que hará que las ruedas empiecen a rodar. Al empezar a rodar, el punto de contacto entre las ruedas y el bloque superior empieza a intentar moverse hacia la izquierda, por lo que aparecerá una fuerza de rozamiento entre ambos cuerpos, tal que se opondrá a dicho movimiento; es decir, irá hacia la derecha sobre las ruedas, y hacia la izquierda sobre el bloque superior.
, que hará que las ruedas empiecen a rodar. Al empezar a rodar, el punto de contacto entre las ruedas y el bloque superior empieza a intentar moverse hacia la izquierda, por lo que aparecerá una fuerza de rozamiento entre ambos cuerpos, tal que se opondrá a dicho movimiento; es decir, irá hacia la derecha sobre las ruedas, y hacia la izquierda sobre el bloque superior.
Comencemos por hacer los diagramas de cuerpo libre para cada cuerpo.

Figura 1. Diagframa de cuerpo libre para el bloque superior. (Haz click para ver la imagen a tamaño real)
Aplicamos la segunda ley de Newton para el movimiento lineal del bloque superior. Utilizamos el criterio que todas las fuerzas hacia arriba o hacia la izquierda son positivas (ojo, normalmente el criterio de signos para el eje horizontal suele ser el contrario). Tenemos, pues
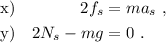
Ambas ruedas son equivalentes, por lo que nos sirve aplicar una única vez la ley de Newton para su movimiento lineal,
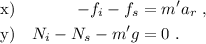
Las ecuaciones para las componentes nos dirán el valor de las fuerzas normales,
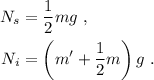
Esto nos permite calcular el valor del rozamiento entre las ruedas y el bloque inferior,
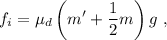
donde 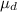 es el coeficiente de rozamiento dinámico entre las ruedas y los bloques.
Nótese que no se puede hacer lo mismo con el rozamiento superior, ya que es estático; sólo sabemos que debe ser
es el coeficiente de rozamiento dinámico entre las ruedas y los bloques.
Nótese que no se puede hacer lo mismo con el rozamiento superior, ya que es estático; sólo sabemos que debe ser 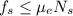 , pero debemos averiguar su valor concreto de otro modo.
, pero debemos averiguar su valor concreto de otro modo.
Las ecuaciones para las componentes verticales nos dan directamente las aceleraciones,
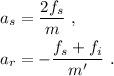
La última ecuación que nos queda por plantear es la del movimiento circular de las ruedas. El centro de la rotación es el centro de masa, y dado que la masa está repartida de forma homogénea, su momento de inercia es 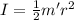 , donde
, donde  es su radio. Tomamos positivo el giro antihorario, con lo cual tenemos
es su radio. Tomamos positivo el giro antihorario, con lo cual tenemos
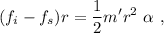
lo que nos da la aceleración angular
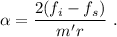
Integrando las ecuaciones (5) y (7) podemos encontrar las velocidades de cada cuerpo.
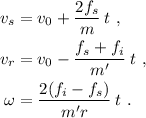
Si el bloque superior no debe deslizarse sobre las ruedas, su velocidad debe ser igual a la velocidad lineal del punto de contacto de las ruedas. El movimiento de dicho punto es la composición de la velocidad del centro de masas de la rueda, 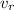 , y de la velocidad debida a la rotación,
, y de la velocidad debida a la rotación, 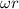 , por lo que la ecuación de no deslizamiento debe ser
, por lo que la ecuación de no deslizamiento debe ser
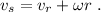
Substituyendo los valores de la ecuación (8), tenemos
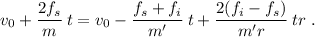
Simplificando,
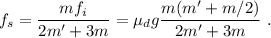
Como hemos dicho, esta fuerza de rozamiento debe ser menor al valor máximo,
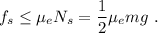
Substituyendo (11), tenemos
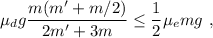
simplificando, encontramos la condición que debe cumplir 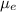 ,
,
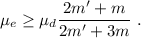
Nótese que la fracción en (14) siempre es menor que uno. El coeficiente estático nunca puede ser menor que el dinámico, por lo que todos los materiales cumplirán esta condición.
El rozamiento inferior seguirá en efecto hasta que el punto de contacto deje de deslizar sobre el bloque inferior, es decir, cuando su velocidad sea cero. Esto se traduce en la condición
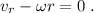
Substituyendo los valores en (8)
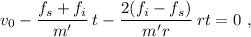
lo que nos da
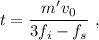
que, en términos de los datos del problema,
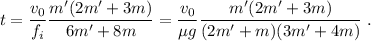
La velocidad lineal final de la rueda será
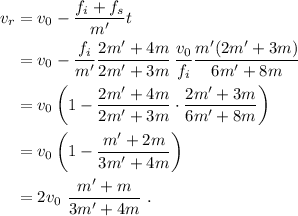
La velocidad angular de la rueda será

Vemos que, naturalmente, se cumple la condición de no deslizamiento,  . Por último, la velocidad del bloque superior es
. Por último, la velocidad del bloque superior es
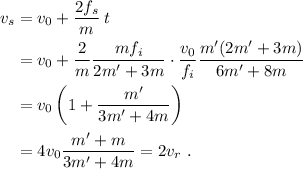
Podíamos haber anticipado la relación 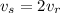 , que es consecuencia de las dos condiciones de no deslizamiento. De hecho, la podemos sacar restando las ecuaciones (9) y (15).
, que es consecuencia de las dos condiciones de no deslizamiento. De hecho, la podemos sacar restando las ecuaciones (9) y (15).
Para este último apartado nos basta con substituir. Para las ruedas
Para el bloque superior,
La variación de la energía cinética total es
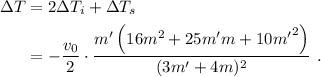
Considere un cilindro de radio  y densidad
y densidad 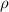 con una perforación cilíndrica de radio
con una perforación cilíndrica de radio 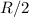 , tal como se muestra en la figura. El cilindro rueda sin resbalar sobre una superficie horizontal realizando pequeñas oscilaciones en torno a su posición de equilibrio. Encuentre el periodo de las oscilaciones.
, tal como se muestra en la figura. El cilindro rueda sin resbalar sobre una superficie horizontal realizando pequeñas oscilaciones en torno a su posición de equilibrio. Encuentre el periodo de las oscilaciones.


 ). La inclinación del plano es de
). La inclinación del plano es de 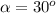 .
.