Problemas de dinámica de la rotación
Nivel: Primer ciclo
En la cima de una gran esfera fija de radio 
se sitúa una pequeña canica maciza, también esférica, de radio 
y masa 
. La canica parte del reposo y cae por la superficie de la esfera mayor sin deslizar. Calcula:
1.La velocidad de la canica en función del ángulo con la vertical.
2.El ángulo que forma con la vertical en el momento en que deja de estar en contacto con la superficie.
3.La fuerza de fricción en función del ángulo
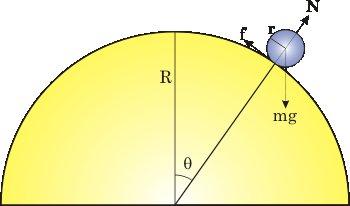
Para comenzar, realizamos el diagrama del problema, incluyendo todas las fuerzas involucradas:
Donde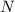 
es la fuerza normal y 
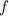la fuerza del fricción.
Todas las fuerzas que intervienen en este problema son conservativas. Por lo tanto, la energía total se conserva. En este caso, tenemos tres contribuciones a la energía: potencial, cinética de translación y cinética de rotación,
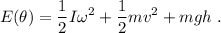
Si tomamos la base de la esfera mayor como origen de energía potencial, tenemos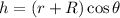 
. Al ser la canica una esfera maciza, su momento de inercia es 
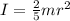. Por último, como la canica baja sin deslizar, tenemos 
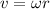. Por lo tanto, tenemos,
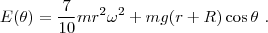
Teniendo en cuenta que en el momento inicial,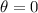 
, la canica empieza en reposo, 
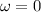. Estamos ya en condiciones de utilizar la conservación de la energía mecánica, 
,
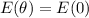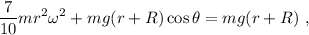
de donde obtenemos
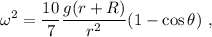
o en términos de la velocidad lineal
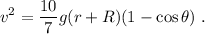
Comenzamos por escribir la expresión de la segunda ley de Newton,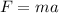 
, en la dirección perpendicular. La aceleración debe ser exactamente la centrípeta, 
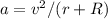; por lo que tenemos
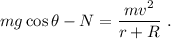
La fuerza normal es justamente la que tiene en cuenta el contacto entre ambas esferas, por lo que en el momento en que se separan debe anularse,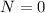 
. Teniendo esto en cuenta, y utilizando la ecuación (5), tenemos
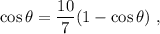
de donde obtenemos
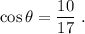
Por lo tanto, la respuesta es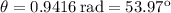 
.
La segunda ley de Newton en la dirección paralela a la superficie de la esfera fija se escribe de la forma
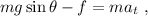
donde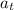 
es la aceleración tangencial. Debemos escribir también la ley de Newton para el movimiento circular al rededor del centro de masas; la única fuerza que contribuye a la rotación es el fricción, ya que el peso se aplica directamente sobre el centro de masas, y la normal es perpendicular al mismo,
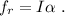
Debido a que la canica se mueve sin deslizar, se cumplirá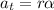 
, por lo que podemos utilizar (10) para obtener el valor de la aceleración tangencial,
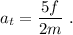
Utilizando esto en (9) obtenemos
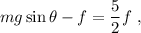
de donde tenemos
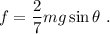
Nótese que escrita de esta forma, la fuerza de fricción no depende de los radios de las esferas. No obstante, en realidad sí depende, a través de la función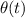 
.
Un disco uniforme de masa 
, radio y espesor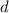 
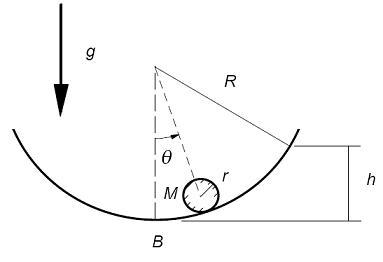
rueda sin resbalar sobre una superficie esférica de radio como se muestra en la figura. El movimiento es plano.
1.Encontrar el tiempo para el cuál el radio vector que une el centro del hemisferio esférico con el centro del disco barre un ángulo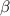 
.
2.Encontrar el periodo para el caso en que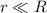 
.
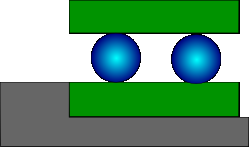
Consideramos el sistema de la figura 1.
El bloque inferior se mueve sobre raíles, con rozamiento despreciable. El sistema de los dos bloques y las dos ruedas se mueven hacia la izquierda de forma solidaria con velocidad constante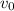 
. En un instante dado, el bloque inferior colisiona con un escalón, de forma que se frena completamente de golpe. Ambos bloques están hechos del mismo material, y son lo suficientemente largos. La masa del bloque superior es , y la de las ruedas 
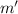. Todos los cuerpos son homogéneos.
1.¿Qué condición debe cumplir el coeficiente de rozamiento entre los bloques y las ruedas para que el bloque superior no deslice sobre ellas?
2.Calcula la velocidad final de cada elemento del sistema.
3.Calcula la variación de energía cinética de cada elemento del sistema.
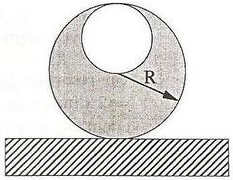
Considere un cilindro de radio y densidad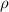 
con una perforación cilíndrica de radio 
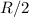, tal como se muestra en la figura. El cilindro rueda sin resbalar sobre una superficie horizontal realizando pequeñas oscilaciones en torno a su posición de equilibrio. Encuentre el periodo de las oscilaciones.
