Problemas de mecánica analítica
1
Nivel
Segundo ciclo
Dificultad
5
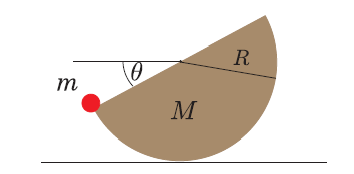
Una semiesfera uniforme de masa  y radio
y radio  se encuentra sobre un plano horizontal. Se coloca en su borde (ver figura) una partícula de masa
se encuentra sobre un plano horizontal. Se coloca en su borde (ver figura) una partícula de masa  . Determine mediante el método de los trabajos virtuales la relación entre las masas si en la posición de equilibro
. Determine mediante el método de los trabajos virtuales la relación entre las masas si en la posición de equilibro 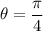 .
.
Solución disponible
José Adrián C M
2
Nivel
Segundo ciclo
Dificultad
6
Una varilla, cuyo centro de masa CM la divide en dos partes de longitudes  y
y 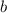 , se encuentra en equilibrio con sus extremos apoyados sobre dos planos inclinados de ángulos
, se encuentra en equilibrio con sus extremos apoyados sobre dos planos inclinados de ángulos 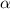 y
y 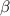 respecto de la horizontal. Mediante el método de los trabajos virtuales, determine el ángulo
respecto de la horizontal. Mediante el método de los trabajos virtuales, determine el ángulo 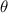 que la varilla forma con la horizontal en la posición de equilibro. El rozamiento es nulo.
que la varilla forma con la horizontal en la posición de equilibro. El rozamiento es nulo.
Solución disponible
José Adrián C M