Problemas de trabajo y energía
Un cuerpo de masa m describe una trayectoria circular con movimiento uniforme. ¿Qué trabajo realiza la fuerza centrípeta en una vuelta?
Una partícula de 5 kg de masa está en una montañana rusa, inicialmente en el punto A, a una altura de 5 m y posee cierta rapidez, sabiendo que la rapidez en el punto B es igual a 15 m/s y la altura de B es igual a 3,2 m; determina la rapidez de la partícula en el punto A.
Dos cuerpos A y B de masas m y 10m respectivamente se mueven sobre una superficie horizontal con idéntica energía cinética. ¿Cuál de ellos tiene mayor momento lineal?
Para hacer este problema, el camino más directo es reescribir la energía cinética a partir de la definición de momento,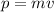 
,
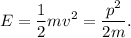
El enunciado nos dice que la energía cinética de los cuerpos A y B son iguales, por lo tanto
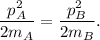
De esta ecuación ya vemos que, para tener la misma energía cinética que A, debido a su mayor masa (que aparece dividiendo), B debe tener mayor momento lineal. Pero comprobemoslo explícitamente.
Reorganizando la ecuación tenemos
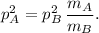
Por último, substituimos los valores de la masa que nos da el enunciado,
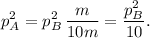
Es decir,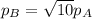 
. Por lo tanto, el cuerpo B tiene mayor momento
En primer lugar, indiquemos las expresiones de la energía cinética de cada cuerpo.
Como ambos cuerpos se mueven con la misma energía cinética, podemos escribir la siguiente igualdad:
Por otro lado, conocemos la relación entre la masa del cuerpo A y la del cuerpo B, siendo ésta:
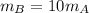
De este modo, podemos sustituir en (3) y así obtener la velocidad del cuerpo A:
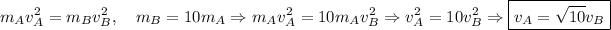
Una vez obtenida la relación de las velocidades de cada cuerpo, podemos comparar cuál de ellos tiene una mayor cantidad de movimiento o momento lineal. Los módulos serán por tanto:
Finalmente, llegamos a la conclusión de que el cuerpo con mayor momento lineal es el cuerpo B:
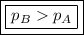
Sobre una partícula actúa la fuerza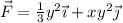 
, donde x e y están expresadas en m, y F en N. Calcula el trabajo realizado por la fuerza cuando la partícula se desplaza desde el punto A(0, 0) hasta el punto B(1, 2) en dos etapas: a lo largo del eje Y, desde el origen hasta el punto (0, 2); y desde aquí paralelamente al eje X hasta el punto B.
Una masa de 3 kg se mueve con una velocidad de 1m/s en la dirección del eje X. Cuando pasa por el origen actúa sobre esta masa una fuerza única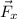 
que varía con x como indica la figura.
1.Determina el trabajo realizado por la fuerza desde x=0 hasta x=3m.
2.Calcula la energía cinética y la velocidad de la masa en el punto x=3m.
Una persona de 60 kg se encuentra en un ascensor. El ascensor inicia la subida con una aceleración de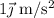 
durante 2s, continuando después con movimiento uniforme durante 10s y desacelerando con 
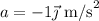durante 2s.
1.Calcular el trabajo realizado por la fuerza normal que ejerce el suelo sobre la persona durante todo el trayecto.
2.Calcular la potencia media que suministra la fuerza normal durante los 14s.
Aunque podemos recurrir a varios procedimientos, uno bastante directo consiste en aplicar el teorema de la energía cinética.
Sobre la persona actúan dos fuerzas: su peso y la normal. Por tanto, la suma de los trabajos realizados por ambas será igual a la variación que experimente la energía cinética. Puesto que inicialmente es nula, bastará con que calculemos la que posee finalmente.
Al cabo de los primeros 2 s la persona alcanzará una velocidad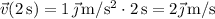 
. Durante los 10 s siguientes mantendrá esta velocidad y por último, en los 2 s finales pasará a tener una velocidad 
.
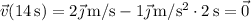Dado que la energía cinética final es igual a la inicial, el trabajo total realizado por ambas fuerzas será nulo. En consecuencia, como el trabajo realizado por el peso es igual al opuesto de la variación de la energía potencial gravitatoria, es decir,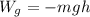 
(donde 
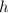es la altura del punto del final del recorrido respecto del de partida), concluimos que la normal habrá realizado un trabajo 
.
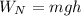La altura 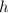será la suma de las alturas ganadas en cada uno de los tres tramos de los que se compone el movimiento. En el primero será 
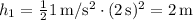. En el segundo será 
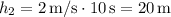. Y en el tercero, 
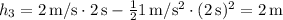. Por tanto, 
.
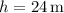Trasladando este resultado a la expresión del trabajo realizado por la normal tenemos que éste será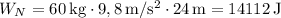 
.
Así pues, la potencia media desarrollada por dicha fuerza será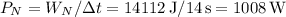 
, esto es, teniendo en cuenta la precisión de los datos del enunciado,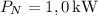 
-----
Una alternativa a la segunda parte de este cálculo podría ser la siguiente: puesto que la potencia media que queremos obtener es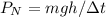 
y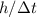 
es la velocidad media, 
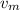, nuestro objetivo es determinar 
.
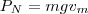En un movimiento uniformemente acelerado la velocidad media es igual a la semisuma de las velocidades inicial y final. En consecuencia, la velocidad media durante los primeros 2 s habrá sido de 1 m/s. Durante los 10 s restantes fue, evidentemente, 2 m/s. Por último, en los 2 s finales habrá sido de nuevo 1 m/s. En consecuencia, la velocidad media para todo el trayecto habrá sido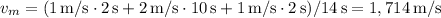 
. De esta manera tenemos que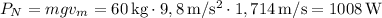 
Hallar el trabajo hecho por la fuerza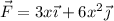 
para elevar un punto material desde el origen hasta el punto (2, 4) m:
1.a lo largo de la recta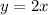 
.
2.a lo largo de la curva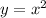 
.
