Problemas de trabajo y energía
Un cuerpo de masa m describe una trayectoria circular con movimiento uniforme. ¿Qué trabajo realiza la fuerza centrípeta en una vuelta?
Una partícula de 5 kg de masa está en una montañana rusa, inicialmente en el punto A, a una altura de 5 m y posee cierta rapidez, sabiendo que la rapidez en el punto B es igual a 15 m/s y la altura de B es igual a 3,2 m; determina la rapidez de la partícula en el punto A.
Dos cuerpos A y B de masas m y 10m respectivamente se mueven sobre una superficie horizontal con idéntica energía cinética. ¿Cuál de ellos tiene mayor momento lineal?
Para hacer este problema, el camino más directo es reescribir la energía cinética a partir de la definición de momento,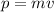 
,
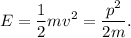
El enunciado nos dice que la energía cinética de los cuerpos A y B son iguales, por lo tanto
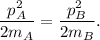
De esta ecuación ya vemos que, para tener la misma energía cinética que A, debido a su mayor masa (que aparece dividiendo), B debe tener mayor momento lineal. Pero comprobemoslo explícitamente.
Reorganizando la ecuación tenemos
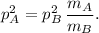
Por último, substituimos los valores de la masa que nos da el enunciado,
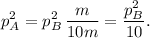
Es decir,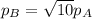 
. Por lo tanto, el cuerpo B tiene mayor momento
En primer lugar, indiquemos las expresiones de la energía cinética de cada cuerpo.
Como ambos cuerpos se mueven con la misma energía cinética, podemos escribir la siguiente igualdad:
Por otro lado, conocemos la relación entre la masa del cuerpo A y la del cuerpo B, siendo ésta:
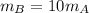
De este modo, podemos sustituir en (3) y así obtener la velocidad del cuerpo A:
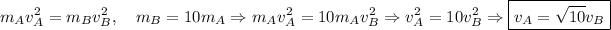
Una vez obtenida la relación de las velocidades de cada cuerpo, podemos comparar cuál de ellos tiene una mayor cantidad de movimiento o momento lineal. Los módulos serán por tanto:
Finalmente, llegamos a la conclusión de que el cuerpo con mayor momento lineal es el cuerpo B:
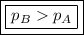
Sobre una partícula actúa la fuerza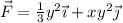 
, donde x e y están expresadas en m, y F en N. Calcula el trabajo realizado por la fuerza cuando la partícula se desplaza desde el punto A(0, 0) hasta el punto B(1, 2) en dos etapas: a lo largo del eje Y, desde el origen hasta el punto (0, 2); y desde aquí paralelamente al eje X hasta el punto B.
Una masa de 3 kg se mueve con una velocidad de 1m/s en la dirección del eje X. Cuando pasa por el origen actúa sobre esta masa una fuerza única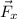 
que varía con x como indica la figura.
1.Determina el trabajo realizado por la fuerza desde x=0 hasta x=3m.
2.Calcula la energía cinética y la velocidad de la masa en el punto x=3m.
Una persona de 60 kg se encuentra en un ascensor. El ascensor inicia la subida con una aceleración de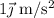 
durante 2s, continuando después con movimiento uniforme durante 10s y desacelerando con 
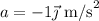durante 2s.
1.Calcular el trabajo realizado por la fuerza normal que ejerce el suelo sobre la persona durante todo el trayecto.
2.Calcular la potencia media que suministra la fuerza normal durante los 14s.
Hallar el trabajo hecho por la fuerza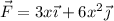 
para elevar un punto material desde el origen hasta el punto (2, 4) m:
1.a lo largo de la recta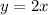 
.
2.a lo largo de la curva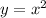 
.
Para calcular el trabajo hecho por la fuerza, procederemos de la siguiente forma:
Calcularemos el trabajo infinitesimal, que es el producto escalar del vector fuerza por el vector desplazamiento, es decir:
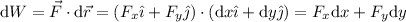
Las variables x e y están relacionadas a través de la ecuación de la trayectoria, cuya forma general es: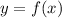
, y que en este caso, distinguiremos entr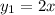e 
e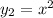 
. Por tanto:
A lo largo de la recta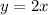
En este caso, tenemos que:
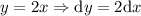
Por tanto, el trabajo infinitesimal será:
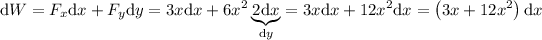
Así pues, el trabajo realizado por la fuerza para elevar el punto a lo largo de la recta es:
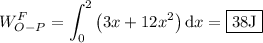
A lo largo de la curva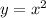 
.
Procedemos de manera similar al anterior apartado, teniendo en cuenta en este caso que:
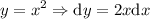
Por tanto, el trabajo infinitesimal será:
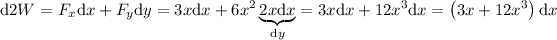
Por último, calculamos el trabajo realizado:
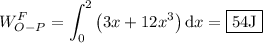
Observamos que el trabajo realizado por la fuerza para elevar el punto material hasta el punto P(2,4) a lo largo de la recta es mayor que el realizado a lo largo de la curva. Es decir, el trabajo depende del camino seguido para ir del punto O(0,0) al punto P(2,4).
De esto, podemos extraer la siguiente conclusión: la fuerza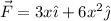 
es una fuerza no conservativa, pues el trabajo depende del camino seguido para ir de un punto A a otro punto B.
Podemos comprobar que la fuerza no es conservativa calculando el rotacional del campo de fuerzas:
Podemos hallarlo mediante el siguiente determinante (nótese que éste es sólo simbólico):
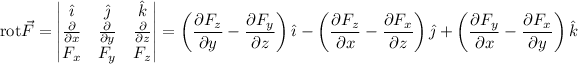
Por tanto:
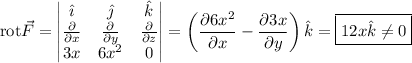
Dado que el rotacional es distinto de cero, la fuerza no es conservativa, tal y como habíamos determinado al observar que el trabajo realizado por la fuerza entre dos puntos dependía de la trayectoria seguida.
