Problemas de trabajo y energía
Un cuerpo de masa m describe una trayectoria circular con movimiento uniforme. ¿Qué trabajo realiza la fuerza centrípeta en una vuelta?
Una partícula de 5 kg de masa está en una montañana rusa, inicialmente en el punto A, a una altura de 5 m y posee cierta rapidez, sabiendo que la rapidez en el punto B es igual a 15 m/s y la altura de B es igual a 3,2 m; determina la rapidez de la partícula en el punto A.
Dos cuerpos A y B de masas m y 10m respectivamente se mueven sobre una superficie horizontal con idéntica energía cinética. ¿Cuál de ellos tiene mayor momento lineal?
Para hacer este problema, el camino más directo es reescribir la energía cinética a partir de la definición de momento,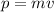 
,
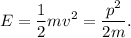
El enunciado nos dice que la energía cinética de los cuerpos A y B son iguales, por lo tanto
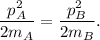
De esta ecuación ya vemos que, para tener la misma energía cinética que A, debido a su mayor masa (que aparece dividiendo), B debe tener mayor momento lineal. Pero comprobemoslo explícitamente.
Reorganizando la ecuación tenemos
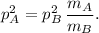
Por último, substituimos los valores de la masa que nos da el enunciado,
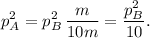
Es decir,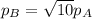 
. Por lo tanto, el cuerpo B tiene mayor momento
En primer lugar, indiquemos las expresiones de la energía cinética de cada cuerpo.
Como ambos cuerpos se mueven con la misma energía cinética, podemos escribir la siguiente igualdad:
Por otro lado, conocemos la relación entre la masa del cuerpo A y la del cuerpo B, siendo ésta:
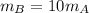
De este modo, podemos sustituir en (3) y así obtener la velocidad del cuerpo A:
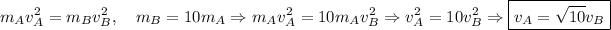
Una vez obtenida la relación de las velocidades de cada cuerpo, podemos comparar cuál de ellos tiene una mayor cantidad de movimiento o momento lineal. Los módulos serán por tanto:
Finalmente, llegamos a la conclusión de que el cuerpo con mayor momento lineal es el cuerpo B:
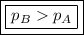
Sobre una partícula actúa la fuerza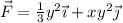 
, donde x e y están expresadas en m, y F en N. Calcula el trabajo realizado por la fuerza cuando la partícula se desplaza desde el punto A(0, 0) hasta el punto B(1, 2) en dos etapas: a lo largo del eje Y, desde el origen hasta el punto (0, 2); y desde aquí paralelamente al eje X hasta el punto B.
Una masa de 3 kg se mueve con una velocidad de 1m/s en la dirección del eje X. Cuando pasa por el origen actúa sobre esta masa una fuerza única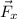 
que varía con x como indica la figura.
1.Determina el trabajo realizado por la fuerza desde x=0 hasta x=3m.
2.Calcula la energía cinética y la velocidad de la masa en el punto x=3m.
Sabemos que el trabajo se calcula matemáticamente con la integral
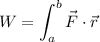
como el movimiento y la fuerza suceden en la misma dirección
podemos escribir la ecuación de la siguiente forma
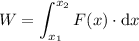
pero aun no hemos hallado la funcion F(x) pero como es una recta podemos hallar su ecuación por semejanza
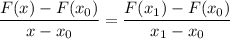
de donde
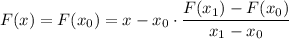
reemplazando los valores que se desprenden del grafico
| x | F(x) |
| 0 | 2 |
| 3 | 3 |
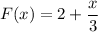
1.calculamos el trabajo entre la posición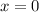 
y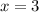 
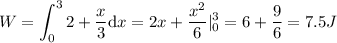
2.la variacion de la energia mecanica es igual al trabajo realizado por la fuerza, por lo tanto la energia cinetica final sera
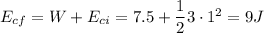por lo que la velocidad final es
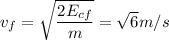
una forma mas complicada de obtenerlo sería
utilizar el equilibrio de fuerzas pues sabemos
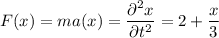
luego
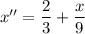
que es una ecuación diferencial no lineal que puede resolverse por variables separadas dando
la siguiente primitiva
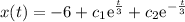
de las condiciones iniciales del problema sabemos que en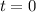 
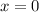
entonces
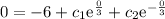
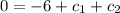
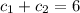
si derivamos la ecuacion 1 con respecto al tiempo llegamos a
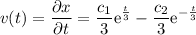
sabiendo que en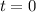 
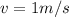
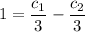
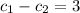
de las ecuaciones 2 y 4 tenemos el siguiente sistema de ecuaciones
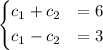
cuya solución es
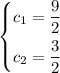
podemos escribir la ecuación 1 de por ma particular como
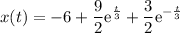
y la ecuación 3 como
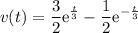
con la ecuación 5 calculamos el tiempo en que 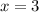se puede resolver graficamente el valor de t y luego ponerlo en la ecuación de la velocidad para calcular la energía cinética o
escribiendo las ecuaciones 5 y 6 de la forma
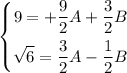
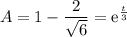
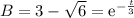
con estas se puede calcular el tiempo t esquivo en las ecuaciones anteriores
Una persona de 60 kg se encuentra en un ascensor. El ascensor inicia la subida con una aceleración de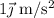 
durante 2s, continuando después con movimiento uniforme durante 10s y desacelerando con 
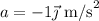durante 2s.
1.Calcular el trabajo realizado por la fuerza normal que ejerce el suelo sobre la persona durante todo el trayecto.
2.Calcular la potencia media que suministra la fuerza normal durante los 14s.
Hallar el trabajo hecho por la fuerza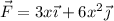 
para elevar un punto material desde el origen hasta el punto (2, 4) m:
1.a lo largo de la recta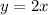 
.
2.a lo largo de la curva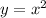 
.
