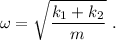Problemas de oscilador armónico simple
El desplazamiento de una partícula viene dado por
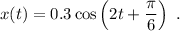
(x en metros y t en segundos).
1.Determinar la frecuencia, el periodo, la amplitud, la pulsación y la fase inicial.
2.¿Dónde se encuentra la partícula en t = 1s?
3.Calcula la velocidad y la aceleración en un instante cualquiera, t.
4.Calcula la posición y velocidad inicial.
Un resorte metálico del que pende una masa m, si se estira ligeramente, comienza a oscilar al dejarlo en libertad. Si cambiamos la masa por otra mayor o menor, ¿se verá afectado el período?, ¿por qué?
Una balanza de resorte, con una constante elástica 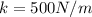 , cuelga verticalmente y una bandeja de
, cuelga verticalmente y una bandeja de 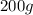 se suspende de su extremo inferior. Un carnicero suelta un filete de
se suspende de su extremo inferior. Un carnicero suelta un filete de 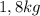 sobre la bandeja desde una altura de
sobre la bandeja desde una altura de 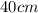 , después de lo cual la bandeja oscila con movimiento armónico simple. Calcular:
, después de lo cual la bandeja oscila con movimiento armónico simple. Calcular:
1.la amplitud,
2.el periodo T,
3.la energía potencial del resorte justo en la posición de equilibrio.
Dibuje el esquema experimental.
Un hilo elástico de constante elástica 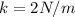 de área transversal igual a
de área transversal igual a 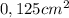 y de
y de 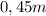 de longitud natural, sostiene verticalmente desde un punto fijo un bloque de
de longitud natural, sostiene verticalmente desde un punto fijo un bloque de 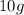 de masa formando un péndulo simple. ¿Cuál es el periodo T de las oscilaciones de este péndulo?
de masa formando un péndulo simple. ¿Cuál es el periodo T de las oscilaciones de este péndulo?
1.En la tierra 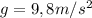 .
.
2.En la luna 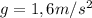 .
.
Dibuje el esquema en cada caso. Suponga en todo momento que durante las oscilaciones la variación de la longitud del hilo es despreciable.
Considera las diferentes asociaciones de muelles que se muestran en la figura 1. Calcula la frecuencia natural de oscilación de cada uno de estos sistemas.
En el primer caso, el desplazamiento de la masa m será igual a la suma de las elongaciones de los dos muelles,
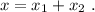
La segunda ley de Newton aplicada al punto de unión entre ambos muelles nos dice
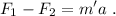
Ahora bien, en el punto de unión entre los muelles no tenemos ninguna masa, m' = 0. Por lo tanto, esto nos daría una aceleración infinita,
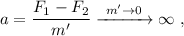
a no ser que la fuerza total también sea cero, lo que implica 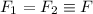 . Por otra parte, está claro que la fuerza que actúa sobra la masa m es precisamente la fuerza del segundo muelle, que por lo tanto también vale F.
. Por otra parte, está claro que la fuerza que actúa sobra la masa m es precisamente la fuerza del segundo muelle, que por lo tanto también vale F.
Obviamente, cada uno de los muelles satisface la ley de Hooke,
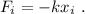
Teniendo esto en cuenta, podemos reemplazar en la ecuación (1),
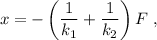
lo que nos da
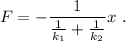
Es decir, la masa m sigue una ley equivalente a la de Hooke, 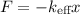 , con una constante efectiva igual a
, con una constante efectiva igual a
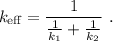
Por lo tanto, la frecuencia de oscilación natural será la equivalente a dicha constante, es decir
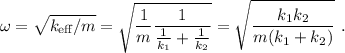
En este caso, ambos muelles tienen la misma longitud, 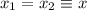 . Cada uno de ellos, transmite su fuerza al bloque, por lo tanto la fuerza total sobre este será la suma,
. Cada uno de ellos, transmite su fuerza al bloque, por lo tanto la fuerza total sobre este será la suma,
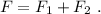
Teniendo en cuenta que cada uno de los muelles cumplen la ley de Hooke tenemos
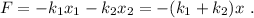
De nuevo, vemos que el sistema se comporta como si hubiera un único muelle con constante efectiva 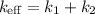 . Por lo tanto, la frecuencia natural será
. Por lo tanto, la frecuencia natural será
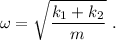
En este último caso, cuando un muelle se encoje, el otro se estira, es decir
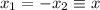
. Además, las fuerzas de cada muelle tienen sentidos opuestos, por lo que la fuerza total sobre el bloque es
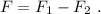
De nuevo, la ley de Hooke para cada muelle nos da
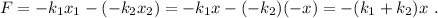
Igual que en los casos anteriores, el sistema se comporta como si sólo existiera un muelle con una constante efectiva 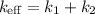 . Por lo tanto, la frecuencia natural es la misma del apartado anterior,
. Por lo tanto, la frecuencia natural es la misma del apartado anterior,