Problemas de inducción matemática
1
Nivel
Secundaria
Dificultad
5
Solución disponible
pod
Paso 1. Para el primer número natural, 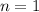 , el sumatorio sólo tiene un término
, el sumatorio sólo tiene un término
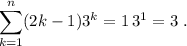
(1)
El lado derecho de la igualdad, por otro lado, es
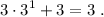
(2)
Por lo tanto, para 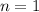 la igualdad se cumple.
la igualdad se cumple.
Paso 2. Por hipótesis de inducción, suponemos que la igualdad se cumple para un n arbitrario,
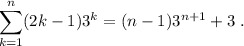
(3)
Paso 3. Haciendo uso de (3), debemos demostrar que se cumple la igualdad para 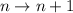 ,
,
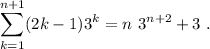
(4)
Para conseguir que (4) se parezca lo más posible a (3), separamos el último término del sumatorio, de esta forma podemos substituir la hipótesis de inducción
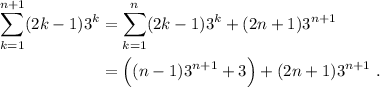
(5)
Sacando factor común de los términos con 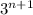 ,
,
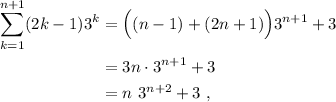
(6)
que coincide con (4), que es lo que queríamos demostrar.
2
Suma de enteros
Nivel
Secundaria
Dificultad
5
Utiliza el principio de inducción para demostrar que la suma de los primeros N números enteros es 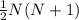 . Es decir,
. Es decir,
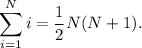
(1)
Solución disponible
Cat_in_a_box
3
Nivel
Primer ciclo
Dificultad
3
Solución disponible
pod
6
Demostración por inducción
Nivel
Primer ciclo
Dificultad
5
Solución disponible
arreldepi
8
Nivel
Primer ciclo
Dificultad
7
Solución disponible
pod
9
Binomio de Newton
Nivel
Primer ciclo
Dificultad
7
Solución disponible
arreldepi
10
Nivel
Primer ciclo
Dificultad
9
Solución disponible
pod

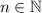 , se cumple
, se cumple
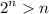 .
.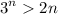 .
.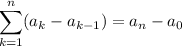 .
.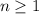
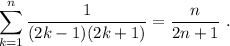
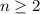 , se cumple
, se cumple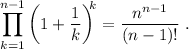
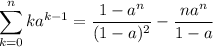
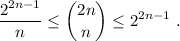
 , terminan en seis.
, terminan en seis.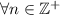 se cumple:
se cumple: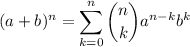
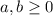 demostrar que para todo
demostrar que para todo 
