Problemas de inducción matemática
Utiliza el principio de inducción para demostrar que la suma de los primeros N números enteros es 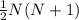 . Es decir,
. Es decir,
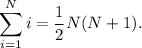
Vamos a proceder por inducción:
- Primero de todo, demostraremos que la hipótesis es cierta para
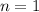
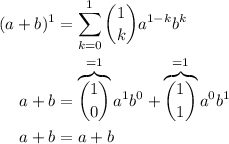 (1)
(1)
- Ahora, vamos a suponer que la hipótesis es cierta para

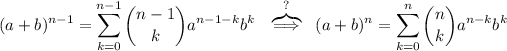 (2)
(2)Es decir, si suponemos que la hipótesis es cierta para
 , debería, también, de ser cierta, para
, debería, también, de ser cierta, para 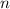 , y eso es lo que vamos a demostrar.
, y eso es lo que vamos a demostrar.
- Demostrémoslo
Tenemos que llegar de la hipótesis que hemos supuesto cierta, es decir,
 , a demostrar que para
, a demostrar que para 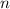 también lo es. Para ello, primero de todo multiplicaremos en ambos lados de la igualdad por el factor
también lo es. Para ello, primero de todo multiplicaremos en ambos lados de la igualdad por el factor 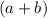 , con lo cual, nos queda:
, con lo cual, nos queda: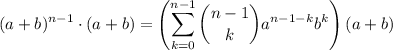 (3)
(3).
En el lado derecho de la igualdad, nos aparece enseguida el término n, en cambio, en el lado izquierdo, aplicando la propiedad distributiva nos queda lo siguiente:
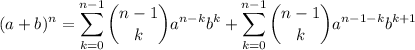 (4)
(4)Para más comodidad, operaremos durante los próximos pasos con las dos sumatorias por separado, con lo cual, llamaremos:
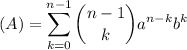
y
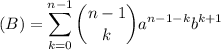
Extrameos el primer elemento (A); es decir, sumaremos des de
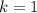 hasta
hasta 
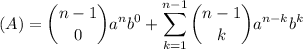 (5)
(5)Extraemos el último término de (B); así que sumaremos des de
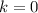 hasta
hasta 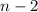 . Antes, haremos el siguiente cambio de variable:
. Antes, haremos el siguiente cambio de variable: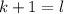 (6)
(6)De manera que, antes de quitarle a (B) el último factor, la sumatoria con el cambio de variable hecho quedaría:
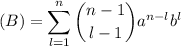 (7)
(7)Es decir, que hemos sumado des de
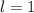 hasta
hasta 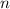 , con lo que vemos, que el número de términos sumados es el mismo que antes.
Ahora, extraemos de la sumatoria el último término y nos queda:
, con lo que vemos, que el número de términos sumados es el mismo que antes.
Ahora, extraemos de la sumatoria el último término y nos queda: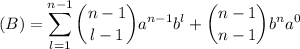 (8)
(8)Por las propiedades de los números combinatorios, sabemos que:
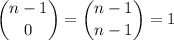 (9)
(9)Con lo cual, si reagrupamos (A) y (B), tenemos que:
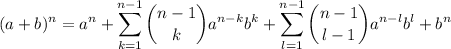 (10)
(10)Como
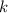 y
y 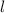 son variables mudas y tienen el mismo recorrido:
son variables mudas y tienen el mismo recorrido:[ERROR DE LaTeX. Error: 4 ]
Podemos decir que
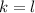 , si reescribimos la igualdad teniendo esto en cuenta:
, si reescribimos la igualdad teniendo esto en cuenta: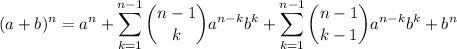 (11)
(11)Que, si tenemos en cuenta las propiedades de las sumatorias, es:
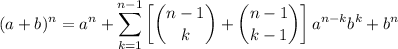 (12)
(12)Por tanto, para completar nuestra demostración, tan sólo tenemos que comprovar que
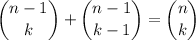 (13)
(13)y sumar de nuevo desde
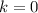 hasta
hasta 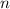 .
.Si desarrollamos los coeficientes binominales, tenemos que:
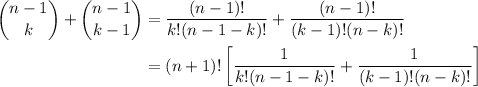 (14)
(14)Como nos interesa tener
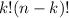 en el denominador, lo haremos aparecer multiplicando y dividiendo por los términos que faltan en cada fracción, es decir:
en el denominador, lo haremos aparecer multiplicando y dividiendo por los términos que faltan en cada fracción, es decir: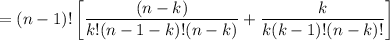 (15)
(15)Como que:
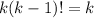 y
y 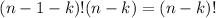
Tenemos que:
[ERROR DE LaTeX. Error: 4 ](16)Por tanto, si reescribimos la igualdad anterior:
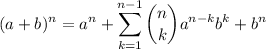 (17)
(17)Y, por último, si introducimos de nuevo el primero y el último término que hemos extraído en (5) y (8) de la sumatoria, volvemos a tener el mismo recorrido, es decir, desde
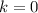 hasta
hasta 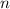 .
.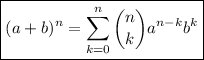 (18)
(18)
Con lo cual, a partir del principio de inducción matemática, hemos demostrado que la hipótesis se cumple 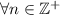

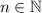 , se cumple
, se cumple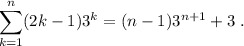

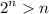 .
.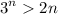 .
.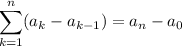 .
.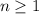
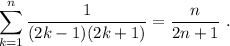
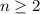 , se cumple
, se cumple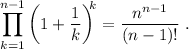
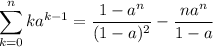
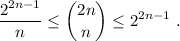
 , terminan en seis.
, terminan en seis.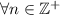 se cumple:
se cumple: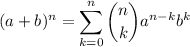
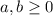 demostrar que para todo
demostrar que para todo 
