Problemas de inducción matemática
Nivel: Primer ciclo
Paso 1. Para 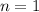 , tenemos
, tenemos 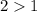 , que obviamente es cierto.
, que obviamente es cierto.
Paso 2. Por hipótesis, suponemos cierta la desigualdad para n arbitrario,
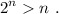
Paso 3. Haciendo uso de lo anterior, debemos demostrar que la desigualdad se cumple para n+1,
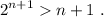
Para hacer esta demostración, comenzamos multiplicando (1) por 2,
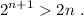
Comparando (2) y (3), vemos que se debe cumplir 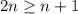 . Esta desigualdad se cumple siempre que
. Esta desigualdad se cumple siempre que 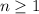 , lo cual es cierto. Esto completa la demostración.
, lo cual es cierto. Esto completa la demostración.
Paso 1. Para 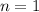 , tenemos
, tenemos 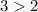 , que obviamente es cierto.
, que obviamente es cierto.
Paso 2. Por hipótesis, suponemos cierta la desigualdad para n arbitrario,
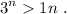
Paso 3. Haciendo uso de lo anterior, debemos demostrar que la desigualdad se cumple para n+1,
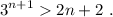
Para hacer esta demostración, comenzamos multiplicando (4) por 3,
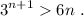
Comparando (5) y (6), vemos que se debe cumplir 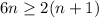 . Esta desigualdad se cumple siempre que
. Esta desigualdad se cumple siempre que 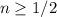 , lo cual es cierto. Esto completa la demostración.
, lo cual es cierto. Esto completa la demostración.
Paso 1. Para 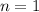 , el sumatorio sólo tiene un término, cuyo valor es precisamente
, el sumatorio sólo tiene un término, cuyo valor es precisamente 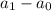 . Por lo tanto, la igualdad se cumple.
. Por lo tanto, la igualdad se cumple.
Paso 2. Suponemos, por hipótesis, la igualdad se cumple para n arbitrario,
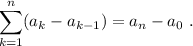
Paso 3. Haciendo uso de (7), debemos demostrar que la igualdad también se cumple por 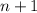 ,
,
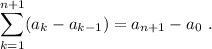
Comenzamos desarrollando el sumatorio de (8), separando el último término (el que tiene 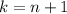 )
)
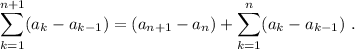
Haciendo uso de (7) sabemos el valor del último sumatorio en (9), por lo que tenemos
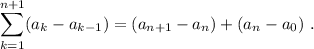
Los términos 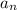 se cancelan mútuamente, quedando únicamente
se cancelan mútuamente, quedando únicamente
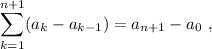
que es exactamente lo que queríamos demostrar.

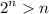 .
.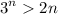 .
.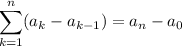 .
.
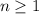
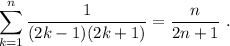
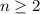 , se cumple
, se cumple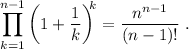
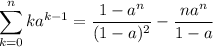
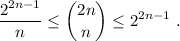
 , terminan en seis.
, terminan en seis.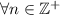 se cumple:
se cumple: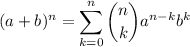
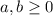 demostrar que para todo
demostrar que para todo 
