Problemas de inducción matemática
Nivel: Primer ciclo
Paso 1. Para n=1 tenemos
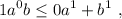
que obviamente es cierto (se cumple la igualdad).
Paso 2. Por hipótesis, suponemos cierta la inecuación para n arbitrario,

Paso 3. Debemos demostrar que (2) implica que la inecuación se cumple para n+1,
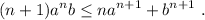
Comenzamos desarrollando el término de la izquierda de (3) para que se parezca lo más posible al de (2),
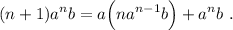
El término entre paréntesis es idéntico al primer miembro de (2), lo que nos permite escribir
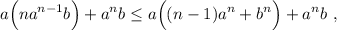
es decir
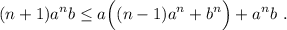
Si somos capaces de demostrar que el segundo miembro de (6) es menor o igual al segundo miembro de (3), entonces tendremos una cadena de desigualdades del estilo 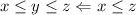 , que demostraría que la ecuación (3) es cierta. Sigamos este camino,
, que demostraría que la ecuación (3) es cierta. Sigamos este camino,
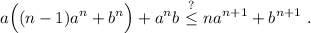
desarrollando,
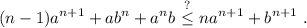
Los términos con 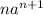 cancelan. Reagrupando el resto de términos,
cancelan. Reagrupando el resto de términos,
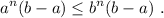
Tenemos tres casos:
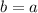 . En este caso, se cumple la igualdad.
. En este caso, se cumple la igualdad.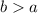 . En este caso, el término entre paréntesis es positivo, por lo que se puede cancelar tranquilamente, dándonos
. En este caso, el término entre paréntesis es positivo, por lo que se puede cancelar tranquilamente, dándonos 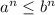 . Dado que la potencia es una función monótona creciente (no cambia el orden de dos números reales), esta desigualdad es coherente: (9) es cierta.
. Dado que la potencia es una función monótona creciente (no cambia el orden de dos números reales), esta desigualdad es coherente: (9) es cierta.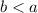 . En este caso, el término entre paréntesis es negativo; para cancelarlo, es necesario cambiar el signo de la desigualdad, por lo que tenemos
. En este caso, el término entre paréntesis es negativo; para cancelarlo, es necesario cambiar el signo de la desigualdad, por lo que tenemos 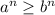 . Según el mismo razonamiento, esta desigualdad sigue siendo coherente: (9) también es cierto en este caso.
. Según el mismo razonamiento, esta desigualdad sigue siendo coherente: (9) también es cierto en este caso.
Como vemos, (9) es cierto en todos los casos. Por lo tanto, (3) es cierta si (2) lo es. Por el principio de inducción, esto completa la demostración.

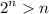 .
.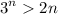 .
.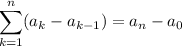 .
.
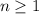
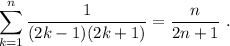
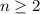 , se cumple
, se cumple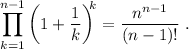
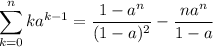
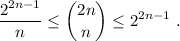
 , terminan en seis.
, terminan en seis.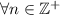 se cumple:
se cumple: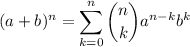
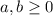 demostrar que para todo
demostrar que para todo 