Problemas de inducción electromagnética
Un conductor recto de 0,2m de longitud se mueve perpendicularmente a un campo magnético uniforme de 1,4T de inducción, con una velocidad de 5m/s. Calcula la fuerza electromotriz inducida y la intensidad que circularía por el conductor si los extremos se conectaran a una resistencia de 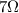 .
.
Un anillo conductor de resistencia 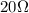 y área
y área 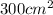 es sometido a un campo magnético perpendicular al anillo y de intensidad variable con el tiempo,
es sometido a un campo magnético perpendicular al anillo y de intensidad variable con el tiempo, 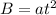 , donde
, donde 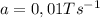 .
.
Calcula la fuerza electromotriz inducida y la potencia eléctrica disipada en un instante 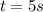 .
.
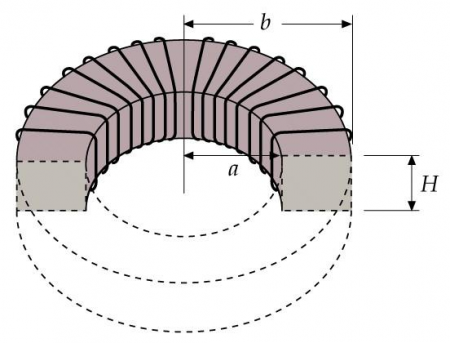
Calcule la inductancia de un toroide de sección rectangular como el que se muestra en la siguiente figura
en función de 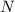 (el número total de vueltas),
(el número total de vueltas),  (el radio interior),
(el radio interior), 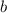 (el radio exterior), y
(el radio exterior), y 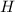 (la altura del toroide).
(la altura del toroide).
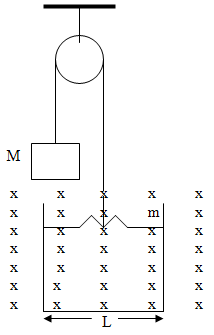
De la polea de masa despreciable de la figura penden a lo largo de una cuerda inextensible y de masa despreciable, una pesa de masa 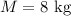 y una varilla conductora ligera, de masa
y una varilla conductora ligera, de masa 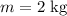 y longitud
y longitud 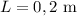 , que está obligada a moverse sobre unos carriles sin rozamiento. La resistencia eléctrica de la varilla es
, que está obligada a moverse sobre unos carriles sin rozamiento. La resistencia eléctrica de la varilla es 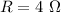 , y la de los carriles se considera despreciable. El campo magnético (
, y la de los carriles se considera despreciable. El campo magnético (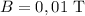 ) que actúa sobre el circuito formado por la varilla y los carriles conductores es perpendicular al plano del papel. Sabiendo que en el instante inicial las masas
) que actúa sobre el circuito formado por la varilla y los carriles conductores es perpendicular al plano del papel. Sabiendo que en el instante inicial las masas  y
y  estaban en reposo, se pide:
estaban en reposo, se pide:
1.Analizar y dibujar las fuerzas que actúan sobre la pesa y la varilla conductora.
2.La velocidad de la varilla en función del tiempo. ¿En qué instante se hace constante la velocidad de la varilla?
3.La aceleración del sistema en función del tiempo y la fuerza electromotriz inducida en función del tiempo.
Problema propuesto en examen de oposiciones a profesor de secundaria, especialidad Física y Química. Castilla-La Mancha, 2002.