Problemas de geometría lineal y espacio afín
Nivel: Secundaria
Tomamos uno de los cuatro puntos como origen, por ejemplo D. Una vez fijado el origen, los otros tres puntos definen otros tantos tres vectores,
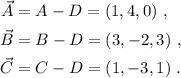
Estos tres vectores definen una matriz,
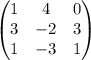
Si el rango de esta matriz es 1, entonces los cuatro puntos están alineados. Si el rango es 2, son coplanares. Si es tres, no son coplanares.
Podemos comprobar fácilmente que el rango es, como mínimo, dos considerando el menor
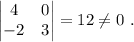
Nos queda únicamenmte comprobar si el rango de la matriz puede ser tres, calculando el determinante total,
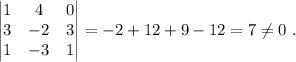
Por lo tanto, el rango de la matriz es tres, y los vectores no son coplanarios.
Dados tres puntos 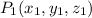 ,
, 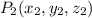 y
y 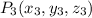 , la ecuación del plano
, la ecuación del plano 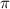 formado por ellos es
formado por ellos es
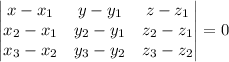
Así, todo punto 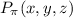 que cumpla lo anterior pertenecerá al plano.
que cumpla lo anterior pertenecerá al plano.
En el caso particular que se nos pide resolvamos, hemos de escribir la matriz con los puntos dados y calcular el determinante; si éste es nulo, entonces los puntos són coplanarios si no, no pertenecerán a un mismo plano.
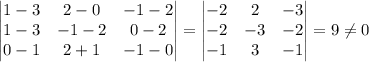
Por lo que los los puntos A(1,2,-1), B(3,0,2), C(1,-1,0) y D(0,2,-1) no son coplanarios.
Dados los planos
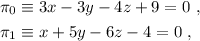
hallar la ecuación de la recta 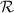 que pasa por el punto
que pasa por el punto  y es paralela a los dos planos.
y es paralela a los dos planos.
En general una recta en el espacio que pasa por el punto 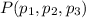 y paralela al vector
y paralela al vector 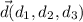 viene dada paramétricamente por
viene dada paramétricamente por
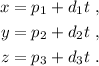
Dados dos planos 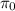 y
y 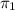 cualquier recta,
cualquier recta, 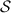 , que cumpla
, que cumpla 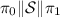 cumple también que
cumple también que 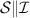 , donde
, donde 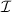 es la recta intersección entre esos dos planos.
es la recta intersección entre esos dos planos.
Sean los planos 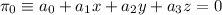 y
y 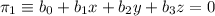 , si tomamos los vectores
, si tomamos los vectores 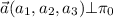 y
y 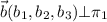 , el vector director,
, el vector director, 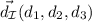 de la recta
de la recta 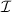 cumplirá que
cumplirá que 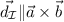 .
.
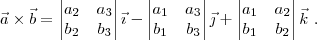
Tomando para simplificar que 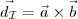 , podemos escribir la recta que nos pedían de la forma:
, podemos escribir la recta que nos pedían de la forma:
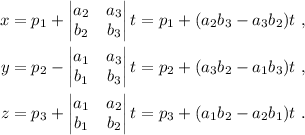
Para el caso particular en que 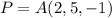 y
y 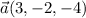 y
y 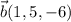 , obtenemos la recta
, obtenemos la recta 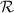
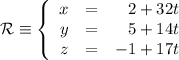

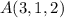 y es perpendicular a la recta
y es perpendicular a la recta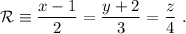

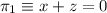 y
y 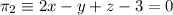 .
.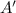 , del punto
, del punto 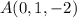 respecto del plano
respecto del plano 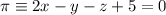 .
.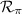 , proyección de la recta
, proyección de la recta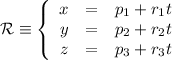
 .
.