Problemas de energía mecánica
Se lanza hacia arriba desde el suelo un cuerpo de 10kg y se observa que alcanza una altura máxima de 2m.
1.¿Con qué energía se lanzó?
2.¿Cuánto vale su energía cinética cuando se encuentra a 1 m de altura?
3.¿Cuánto vale dicha magnitud al llegar de nuevo al suelo?
4.¿De dónde procede y en qué se transforma?
Demostrar, aplicando el teorema de conservación de la energía mecánica, que si lanzamos un cuerpo A verticalmente hacia arriba con velocidad triple que otro B, la altura alcanzada por A es nueve veces la de B.
Se lanza un bloque hacia arriba por un plano inclinado y, después de recorrer cierta distancia, se detiene y se desliza hace abajo la misma distancia. ¿Qué relación existe entre los trabajos realizados por la gravedad al ascender y descender el bloque?
Nota preliminar: aunque es común referirse a "trabajo realizado por la gravedad" en rigor el concepto de trabajo se refiere a fuerzas, por lo que debe entenderse como "trabajo realizado por el peso"
Son opuestos:
Un modo inmediato de demostrarlo parte del hecho de que el peso es una fuerza conservativa, por lo que el trabajo que realiza al trasladar una partícula desde un punto A hasta otro B es igual al opuesto de la variación de la energía potencial gravitatoria, 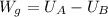 . Si se realiza un desplazamiento opuesto, que nos lleve desde B hasta A, el nuevo trabajo realizado por el peso será, análogamente,
. Si se realiza un desplazamiento opuesto, que nos lleve desde B hasta A, el nuevo trabajo realizado por el peso será, análogamente, 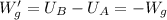 .
.
Es interesante destacar que este resultado es absolutamente general, aunque la gravedad en los puntos A y B sea notoriamente diferente, e independiente de cómo se realice el desplazamiento entre ambos.
Por otra parte, en el caso particular del enunciado podemos hacer uso de un segundo enfoque, aprovechando el hecho de que, al ser uniforme la gravedad, el peso del cuerpo será una fuerza constante, con lo que el trabajo que realiza se puede calcular con el producto escalar entre la fuerza y el desplazamiento, 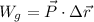 . Como en el retorno se cumple que
. Como en el retorno se cumple que 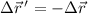 resulta inmediato que
resulta inmediato que 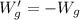 .
.
Sobre un plano que está inclinado un angulo 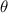 , se sitúa una masa
, se sitúa una masa  que se desliza una distancia
que se desliza una distancia 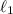 hasta la base del plano. Después recorre una distancia
hasta la base del plano. Después recorre una distancia 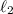 antes de chocar con un resorte de constante de elasticidad
antes de chocar con un resorte de constante de elasticidad 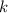 . ¿Cuanto se comprime el resorte si ambas superficies presentan un coeficiente de rozamiento
. ¿Cuanto se comprime el resorte si ambas superficies presentan un coeficiente de rozamiento 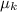 ?
?
Utiliza la conservación de la energía para encontrar la evolución temporal de un oscilador armónico unidimensional, sometido al potencial 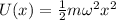 .
.
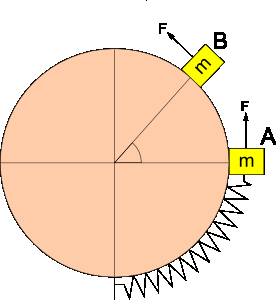
Sobre la superficie lateral de un cilindro liso de radio y longitud se halla un resorte de constante elástica y masa despreciable, unido a una masa, tal y como se ve en la figura.
En la posición A el resorte no está estirado. Mediante fuerzas externas, se lleva lentamente la masa hasta la posición B, indicada por el ángulo en la figura 1. En todo instante la masa esta unida al resorte. Hallar el trabajo que realizan las fuerzas externas sobre la masa.


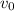 , el módulo de la velocidad
, el módulo de la velocidad  de un proyectil balístico es la misma en todos los puntos a la misma altura, cualquiera que sea el ángulo de disparo.
de un proyectil balístico es la misma en todos los puntos a la misma altura, cualquiera que sea el ángulo de disparo.