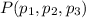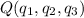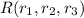El plano que pasa por los tres puntos no alineados , y ; entonces su ecuación puede ser escrita como:

(1)

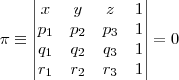
Si desarrollamos el determinante por la primera fila:

(2)

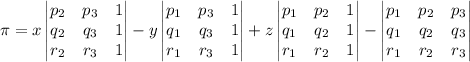
Llamando

(3)

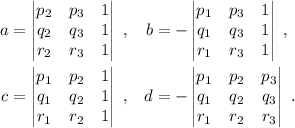
Podemos reescribir (3) como sigue

(4)

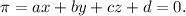
Que es la ecuación del plano que pasa por los puntos P, Q y R no colineales.

Para el caso particular, dados los vectores A(0,1,1), B(2,1,0) y C(3,0,1), calcularemos los coeficientes a, b, c y d por separado y luego los introduciremos en (4); así

(5)

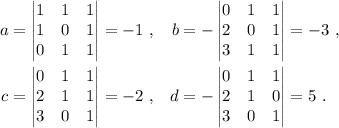
Podemos, por lo tanto, escribir la ecuación del plano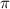

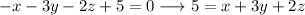
(6)

Volviendo a la expresión general del plano, (4), y tomando dos puntos del mismo 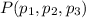y 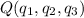para los cuales se cumple la ecuación, es decir:

(7)

(8)

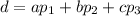
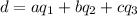
Si restamos las expresiones y sacamos factor común nos queda

(9)

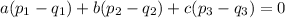
Y teniendo en cuenta que el vector 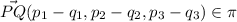, podemos escribir lo anterior como

(10)

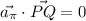
Siendo 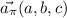y por lo tanto perpendicular al plano, 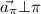. Si aplicamos el resultado obtenido de forma general al plano que teníamos, obtenemos un vector perpendicular a este: .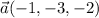