Problemas de leyes de newton en más de una dimensión
Un objeto de masa 7.3kg experimenta una aceleración 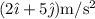 . Encontrar la magnitud de la fuerza (en newton) que actúa sobre el objeto.
. Encontrar la magnitud de la fuerza (en newton) que actúa sobre el objeto.
Dadas las fuerzas siguientes: 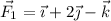 ,
, 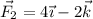 ,
, 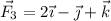 , calcular:
, calcular:
1.La fuerza resultante.
2.Su módulo.
3.Ángulos que forma la fuerza resultante con los ejes cartesianos.
4.Vector unitario de la misma.
5.La fuerza adicional que hay que aplicar para que la nueva resultante sea nula.
1. Para calcular la fuerza resultante, no tenemos más que hacer la suma vectorial de las fuerzas dadas. Así pues:
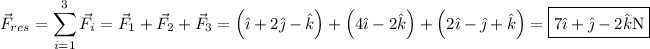
2. El módulo de la fuerza resultante, será por tanto:
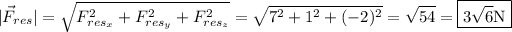
3. Para hallar los ángulos que forma la fuerza resultante con los ejes cartesianos, podemos hallar los cosenos directores. En una base ortonormal, (estamos trabajando con la denominada base canónica),se llaman cosenos directores de un vector a los cosenos de los ángulos que forma el vector con los vectores de la base. Por tanto, una vez obtenidos dichos cosenos, podemos hallar el ángulo:
Cabe destacar que se ha de verificar que:
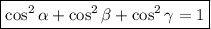
4. Lo primero que hemos de tener claro es que un vector unitario tiene de módulo la unidad. Así pues, la normalización de un vector consiste en asociarle otro vector unitario, de la misma dirección y sentido que el vector dado, dividiendo cada componente del vector por su módulo. Por tanto, un vector unitario de la fuerza resultante será:
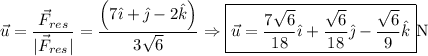
5.La fuerza adicional que hay que aplicar para que la nueva resultante sea nula es justamente: 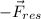 . Por tanto:
. Por tanto:
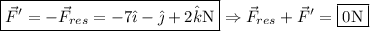
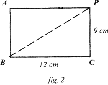
Una partícula, situada en el punto P de la figura 1, es atraída hacia A con una fuerza de 5 N. Al mismo tiempo, es repelida desde el punto B y de C con una fuerza de 15 N. Calcula la fuerza resultante resultante.
Sobre una partícula de 3 kg actúa una fuerza 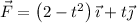 (N). En el instante t = 0 la partícula se encuentra en el punto (4, 1) m, moviéndose con una velocidad
(N). En el instante t = 0 la partícula se encuentra en el punto (4, 1) m, moviéndose con una velocidad 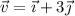 (m/s), determinar al cabo de 1 s:
(m/s), determinar al cabo de 1 s:
1.la posición de la partícula
2.el momento lineal y el momento angular de la partícula respecto al origen.
Un péndulo inextensible de longitud l=0,5 m lleva en su extremo una masa puntual m. Separado de su posición de equilibrio hasta formar un ángulo de 60º con la vertical, se abandona libremente. Cuando pasa por la vertical (punto O), la masa se desprende, quedando el cuerpo bajo la acción de la gravedad. Si desde el punto P al suelo hay una distancia de 2m, calcular:
1.La velocidad en O.
2.La ecuación de la trayectoria de la masa después de romper el hilo y el tiempo que tarda en llegar al suelo. (Tomar como origen el punto O).
Con la ayuda de una cuerda se hace girar un cuerpo de 1kg en una circunferencia vertical de 1m de radio en el que su centro está situado 10,8cm encima del suelo horizontal. La cuerda se rompe cuando la tensión es de 11,2kp, lo que sucede cuando el cuerpo está en el punto más bajo de su trayectoria. Calcula:
1.Tiempo que tarda en caer al suelo.
2.Velocidad cuando se rompe la cuerda y en el instante de chocar con el suelo
Se lanza una bola con una velocidad de 25m/s, formando un ángulo de 53º por encima de la horizontal:
1.¿A qué altura chocará con un muro vertical que está a 30m de distancia?
2.¿Cuál es su velocidad en el momento del choque?
3.Altura máxima alcanzada
Se determina el trabajo realizado por una fuerza entre dos puntos de una trayectoria por diferentes caminos obteniéndose el mismo resultado. ¿Qué significado tiene?
El vector de posición de una partícula de masa 5kg viene dado por la expresión 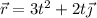 (m) respecto a un sistema de referencia inercial. Calcula:
(m) respecto a un sistema de referencia inercial. Calcula:
1.fuerza que actúa sobre la partícula.
2.momento de dicha fuerza con respecto al origen de coordenadas.
3.momento angular de la partícula con respecto al origen.
4.comprobar si se cumple el teorema de conservación del momento angular.




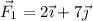 (N) y
(N) y 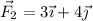 (N). Se pide:
(N). Se pide: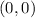 con velocidad
con velocidad 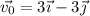 (m/s), ¿qué posición ocupará al cabo de 1 min?
(m/s), ¿qué posición ocupará al cabo de 1 min?