Problemas de integración por residuos
Nivel: Primer ciclo
1
Integración por residuos
Nivel
Primer ciclo
Dificultad
5
Solución disponible
Tupaka
4
Nivel
Primer ciclo
Dificultad
7
Solución disponible
Tupaka
La integral tiene un punto de ramificación de 0 a 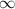 debido al término
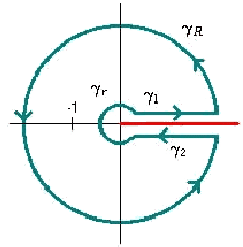
debido al término 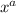 . Por lo tanto, tenemos que intentar rodear todo el corte. La opción más común es tomar el circuito
. Por lo tanto, tenemos que intentar rodear todo el corte. La opción más común es tomar el circuito 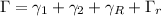 :
:
El único residuo dentro de este circuito se encuentra en 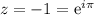 . Nos queda, definiendo
. Nos queda, definiendo 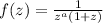 :
:
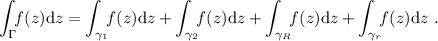
(1)
En 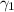 tenemos
tenemos  , mientras que en
, mientras que en 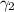 tenemos
tenemos 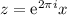 . Además, vemos tanto para
. Además, vemos tanto para 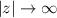 el integrando se anula,
el integrando se anula, 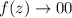 , por lo que la integral en
, por lo que la integral en 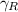 . Por último, para evaluar la integral en
. Por último, para evaluar la integral en 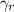 hacemos el cambio
hacemos el cambio 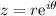 , lo que nos da
, lo que nos da
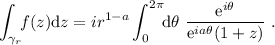
(2)
Para 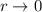 , esta integral se anula. En resumen:
, esta integral se anula. En resumen:
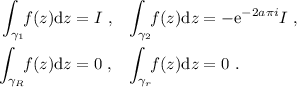
(3)
Por lo tanto, nos queda
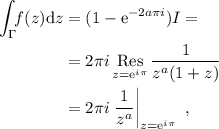
(4)
es decir,
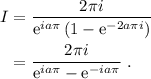
(5)
En definitiva,
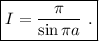
(6)

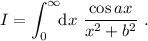

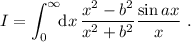
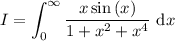
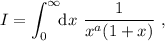
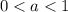 .
.