Problemas de inducción matemática
Utiliza el principio de inducción para demostrar que la suma de los primeros N números enteros es 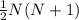 . Es decir,
. Es decir,
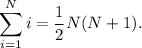
Comencemos por desarrollar lo que significa el sumatorio,
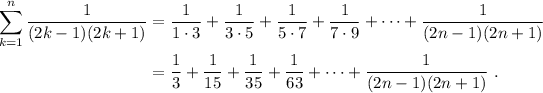
Paso 1. Debemos comprobar que la igualdad se cumple para el primer valor, 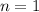 . En este caso, el sumatorio sólo tiene un sumatorio,
. En este caso, el sumatorio sólo tiene un sumatorio,
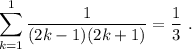
El lado derecho de la igualdad es
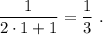
Paso 2. Hacemos la hipótesis de inducción, es decir, suponemos que la igualdad se cumple para n arbitrario,
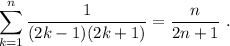
Paso 3. Haciendo uso de (4), debemos demostrar que la igualdad se cumple para n+1,
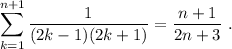
Empezaremos, de nuevo, desarrollando el sumatorio,
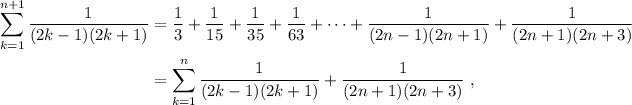
vemos que, excepto el último término, el resto del sumatorio es idéntico al de (4), por lo que podemos substituir,
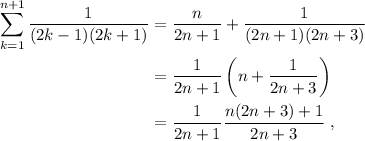
debemos simplificar el polinomio que aparece en el numerador, 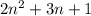 . Utilizamos el procedimiento de Ruffini,
. Utilizamos el procedimiento de Ruffini,
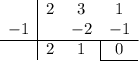
y, por lo tanto,
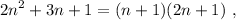
y nos queda
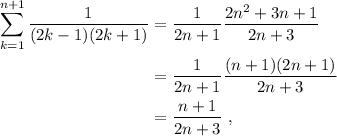
que coincide con (5), por lo tanto si (4) es cierto, también lo es (5). Esto completa la demostración por inducción.

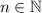 , se cumple
, se cumple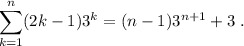

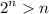 .
.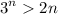 .
.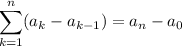 .
.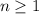
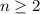 , se cumple
, se cumple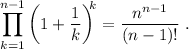
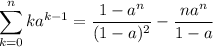
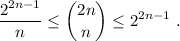
 , terminan en seis.
, terminan en seis.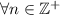 se cumple:
se cumple: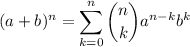
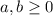 demostrar que para todo
demostrar que para todo 
