Problemas de estática
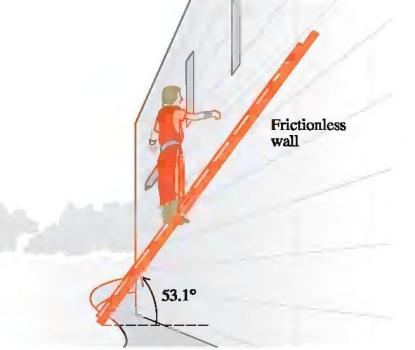
Sir Lancelot está intentando rescatar a Lady Elayne del castillo de Von Doom trepando una escalera de 5m de largo cuyo peso es de 180N. Lancelot, que pesa 800N, se para cuando ha recorrido un tercio de la escalera (véase fig). El final de la escalera descansa en un suelo horizontal y se halla en equilibrio, cruzada y apoyada contra una pared de fricción nula. La escalera forma un ángulo de 53.1º con la horizontal, y forma un triángulo rectángulo de lados 3, 4, y 5m respectivamente.
1.Encuentra la fuerza normal y las fuerzas de fricción de la escalera en la base.
2.Encuentra el valor mínimo del coeficiente estático de rozamiento necesario para que la escalera no resbale y Lancelot impacte contra el suelo.
3.Encuentra la dirección y módulo de la fuerza de contacto de la escalera en la base.
Queremos formar un castillo de cartas. La longitud de cada uno de los naipes es 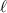 y su masa es
y su masa es  . Las cartas se colocan formando un ángulo
. Las cartas se colocan formando un ángulo 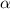 con el suelo.
con el suelo.
1.Para empezar, juntamos dos cartas tal y como se ve en la figura 1a. Calcula el mínimo valor del coeficiente de fricción estático necesario.
2.A continuación, repetimos la misma estructura y situamos encima una carta horizontal, como vemos en la figura 1b. ¿Cuál es el nuevo valor mínimo para el coeficiente de rozamiento?
3.Por último, utilizamos 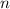 columnas formadas por dos cartas. Sobre ellas, situamos
columnas formadas por dos cartas. Sobre ellas, situamos  naipes horizontales, como vemos en la figura 1c. ¿Cuál es ahora el coeficiente de rozamiento dinámico necesario? Supón que el peso de las cartas horizontales se distribuye de forma uniforme.
naipes horizontales, como vemos en la figura 1c. ¿Cuál es ahora el coeficiente de rozamiento dinámico necesario? Supón que el peso de las cartas horizontales se distribuye de forma uniforme.
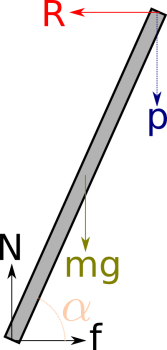
Comencemos por hacer el diagrama de cuerpo libre de una carta y enumerar las fuerzas aplicadas sobre ella:
- Peso, mg. Aplicado en el centro de masas (color oro en el diagrama).
- Fuerza de rozamiento, f. Aplicado en el punto de contacto con el suelo. La dibujamos hacia la derecha ya que al caer la carta, el punto de contacto tiende a desplazarse hacia la izquierda.
- Fuerza normal con el suelo, N.
- Fuerza de contacto con la otra carta (reacción), R. Aplicada sobre el punto superior (color rojo en el diagrama)
- Peso de las cartas horizontales, p. Aplicada sobre el punto superior (color azul en el mapa). Sólo aparece en el segundo y tercer apartado.
El sistema será estable si la suma de todas las fuerzas y torques es cero. En la dirección vertical, el peso y la normal deben compensarse,
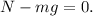
En la dirección horizontal, la reacción de la otra carta debe ser compensada por la fuerza de fricción,
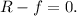
En tercer lugar, la suma de todos los momentos de fuerza también debe anularse. Podemos calcular el momento respecto de cualquier punto, el resultado final del problema debe ser el mismo. Para simplificar el cálculo, tomaremos como origen el punto de contacto de la carta con el suelo, de esta forma el rozamiento y la normal no contribuyen al momento.
El torque se define como el producto vectorial entre el vector que describe el punto de aplicación y la fuerza,
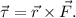
El módulo es igual a la distancia desde el origen hasta el punto de aplicación,  , multiplicado por el módulo de la fuerza y el seno del ángulo entre ambos vectores (tomado en el sentido más corto),
, multiplicado por el módulo de la fuerza y el seno del ángulo entre ambos vectores (tomado en el sentido más corto),
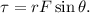
Si nos limitamos a calcular el módulo, debemos añadir el signo a mano siguiendo un convenio. Nosotros eligiéremos positivos los momentos que tienden a provocar un giro en el sentido contrario a las agujas del reloj. La figura 2 nos ayudará a obtener el ángulo necesario en cada caso.
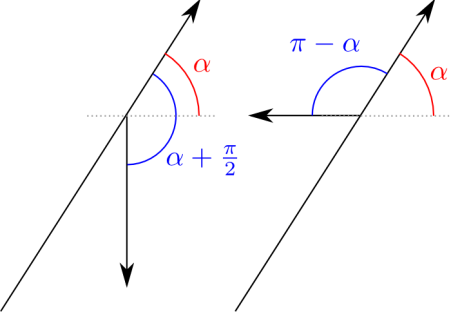
Figura 2. Ángulos necesarios para el producto vectorial. (Haz click para ver la imagen a tamaño real)
Como hemos dicho, como el rozamiento y la normal se aplican sobre el origen (distancia 0), no producen momento. Comencemos por calcular el torque ejercido por el peso. El punto de aplicación esta a una distancia 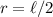 , por lo que tenemos
, por lo que tenemos
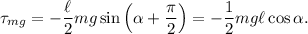
Donde hemos elegido el signo negativo ya que el peso tiende a hacer girar la carga en el sentido de las agujas del reloj. En el caso de la fuerza de reacción tenemos
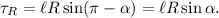
Nota: Algunos alumnos tienen dificultades al realizar este tipo de cálculos con ángulos. Siempre podemos recurrir a realizar el producto vectorial completo. Hagamos el ejemplo del peso. El vector de posición es 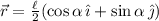 , mientras que el peso es
, mientras que el peso es 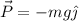 , con lo que tenemos
, con lo que tenemos
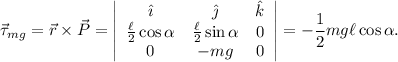
Por lo tanto, si forzamos que la suma de momentos es cero obtenemos nuestra tercera ecuación
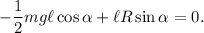
Además, como nos queremos situar en el caso límite, impondremos que la fuerza de rozamiento es la máxima posible, 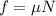 .
.
Ya podemos comenzar a resolver ecuaciones. De (1) tenemos 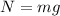 . De (2) obtenemos
. De (2) obtenemos 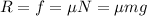 . Si metemos todo esto en (8) obtenemos
. Si metemos todo esto en (8) obtenemos
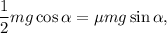
de donde obtenemos
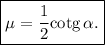
En este apartado añadimos una carta soportada por dos columnas, cada una formada por dos cartas. Suponiendo que el peso de la carta superior se reparte de forma equitativa entre cada una de las cuatro cartas que la soportan (dos por cada columna), la fuerza a añadir en nuestro diagrama de cuerpo libre es 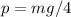 . Esta nueva fuerza entra en nuestras ecuaciones de forma prácticamente idéntica al peso, con la salvedad que su punto de aplicación está a una distancia
. Esta nueva fuerza entra en nuestras ecuaciones de forma prácticamente idéntica al peso, con la salvedad que su punto de aplicación está a una distancia 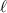 . Por lo tanto, nuestro nuevo sistema de ecuaciones es
. Por lo tanto, nuestro nuevo sistema de ecuaciones es
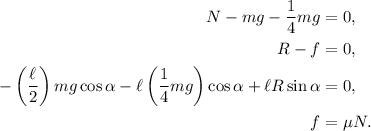
Utilizando la primera, segunda y cuarta ecuación tenemos
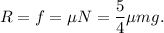
Metiendo todo esto en la tercera ecuación,
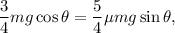
de donde obtenemos
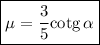
Como es natural, en este caso el coeficiente de fricción necesario es ligeramente superior al apartado anterior.
El peso total del segundo piso, 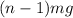 , se reparte sobre las
, se reparte sobre las 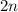 cartas que forman las
cartas que forman las 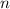 columnas. Por lo tanto, en este caso
columnas. Por lo tanto, en este caso
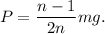
Las ecuaciones son completamente análogas a las del caso anterior, tenemos
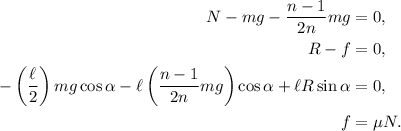
La primera ecuación nos da
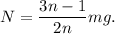
Con esto, la segunda y cuarta ecuación nos dan
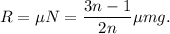
Antes de insertar esto en la tercera ecuación, simplifiquemosla un poco
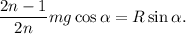
Ahora sí, usando el valor de R tenemos
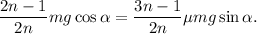
Por lo tanto, tenemos
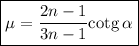
Por supuesto, substituyendo 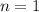 y
y 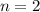 recuperamos los resultados de los apartados anteriores.
recuperamos los resultados de los apartados anteriores.