Problemas de estática
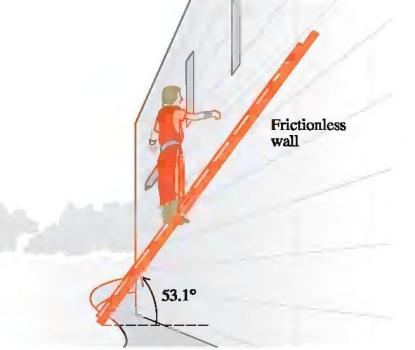
Sir Lancelot está intentando rescatar a Lady Elayne del castillo de Von Doom trepando una escalera de 5m de largo cuyo peso es de 180N. Lancelot, que pesa 800N, se para cuando ha recorrido un tercio de la escalera (véase fig). El final de la escalera descansa en un suelo horizontal y se halla en equilibrio, cruzada y apoyada contra una pared de fricción nula. La escalera forma un ángulo de 53.1º con la horizontal, y forma un triángulo rectángulo de lados 3, 4, y 5m respectivamente.
1.Encuentra la fuerza normal y las fuerzas de fricción de la escalera en la base.
2.Encuentra el valor mínimo del coeficiente estático de rozamiento necesario para que la escalera no resbale y Lancelot impacte contra el suelo.
3.Encuentra la dirección y módulo de la fuerza de contacto de la escalera en la base.
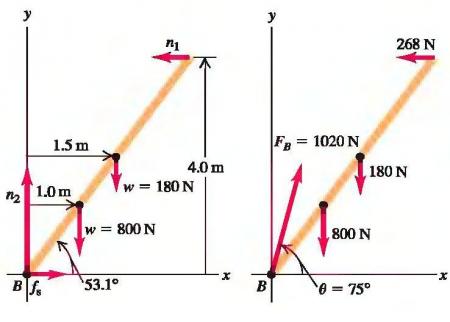
Dado que el sistema Lancelot-escalera no se mueve, podemos usar las dos condiciones de equilibrio para resolver el apartado a). La figura adjunta muestra el diagrama de fuerzas. Se ha tomado el sentido de las agujas del reloj como positivo para considerar los momentos M. Dado que la escalera es uniforme, su centro de gravedad coincide con su centro geometrico. Lancelot ejerce una fuerza (peso) sobre la escalera en un punto situado a un tercio entre la base y la pared.
La pared sin fricción ejerce solo una fuerza normal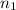 
en la parte alta de la escalera. Las fuerzas en la base son la fuerza normal 
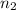dirigida hacia arriba, y la fuerza de fricción estática 
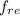que debe apuntar hacia la derecha para prevenir que la escalera no deslice y caiga. El valor de dicha fuerza es 
.
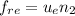De la condición de equilibro, usando la segunda ley de Newton por componentes, tenemos:
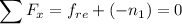
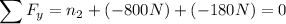
Esto nos deja 3 incógnitas para 2 ecuaciones. Aún así, podemos obtener que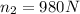 
Sin embargo, necesitamos otra ecuación para poder hallar la solución. Vamos a usar la condición de que dado un punto de referencia, la suma de los momentos M será nula.
Una elección inteligente es elegir el punto B, que nos da el mínimo número de incógnitas y de ecuaciones. Esto es porque las fuerzas 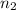y
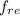no poseen un momento respecto de dicho punto.
De la figura, vemos que la distancia al punto B del peso de la escalera son 1.5m, respecto del peso de Lancelot es 1m y respecto a 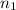son 4m. Con todo esto, la ecuación de la suma de los momentos en torno al punto B, queda como sigue:
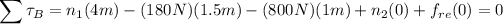
Resolviendo la ecuación, hallamos que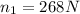 
. Si substituimos eso en la ecuación anterior para el sumatorio de las fuerzas en el eje X, obtenemos que 
.
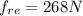La fuerza estática de rozamiento 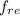no puede exceder un valor mínimo 
de forma que el valor mínimo para el coeficiente estático de rozamiento para evitar el deslizamiento y la caída será:
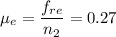
Las componentes de la fueza de contacto en B en la base, son la fuerza estática de rozamiento 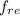y 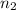de forma que:
El módulo de la fuerza es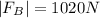 
y la direción viene dada por la arcotangente de la componente y dividida entre la x como ya sabemos y vale: 
.
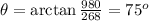Queremos formar un castillo de cartas. La longitud de cada uno de los naipes es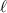 
y su masa es 
. Las cartas se colocan formando un ángulo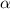 
con el suelo.
1.Para empezar, juntamos dos cartas tal y como se ve en la figura 1a. Calcula el mínimo valor del coeficiente de fricción estático necesario.
2.A continuación, repetimos la misma estructura y situamos encima una carta horizontal, como vemos en la figura 1b. ¿Cuál es el nuevo valor mínimo para el coeficiente de rozamiento?
3.Por último, utilizamos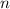 
columnas formadas por dos cartas. Sobre ellas, situamos 
naipes horizontales, como vemos en la figura 1c. ¿Cuál es ahora el coeficiente de rozamiento dinámico necesario? Supón que el peso de las cartas horizontales se distribuye de forma uniforme.
