Problemas de campo eléctrico estático
Nivel: Primer ciclo
Utiliza el teorema de Gauss para calcular el campo eléctrico creado por un hilo cargado de longitud infinita.
Utiliza el teorema de Gauss para calcular el campo eléctrico creado por una esfera de radio R con una carga q uniformemente distribuida.
En cierta región del espacio, el potencial eléctrico viene dado por
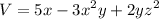
en unidades SI.
1.Calcule las expresiones de las componentes  ,
, 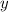 y
y  del campo eléctrico en dicha región del espacio.
del campo eléctrico en dicha región del espacio.
2.¿Cuál es el módulo del campo en el punto 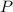 de coordenadas
de coordenadas 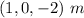 ?
?
3.El punto 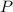 y el
y el 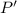 de coordenadas
de coordenadas 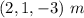 están unidos por un conducto rígido, por el que se puede mover, sin rozamiento, una esfera pequeña de
están unidos por un conducto rígido, por el que se puede mover, sin rozamiento, una esfera pequeña de 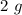 , que tiene una carga
, que tiene una carga 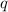 desconocida. Cuando se abandona en reposo dicha esfera en el punto
desconocida. Cuando se abandona en reposo dicha esfera en el punto 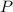 , se observa que llega a
, se observa que llega a 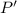 con una velocidad de
con una velocidad de 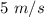 . ¿Cuál es el signo de la carga?, ¿y su valor? No considere el campo gravitatorio.
. ¿Cuál es el signo de la carga?, ¿y su valor? No considere el campo gravitatorio.
En las proximidades de la superficie terrestre existe un campo eléctrico radial dirigido hacia el centro de la Tierra y cuya intensidad media vale 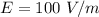 .
.
1.Suponiendo que el globo terrestre se comporta como un buen conductor, determinar la carga total acumulada en su superficie y su signo. ( )
)
2.Debido a la acción de la radiación cósmica y las partículas del viento solar, la atmósfera se ioniza dando lugar a una distribución de carga positiva que puede aproximarse mediante la expresión
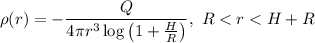
donde  es la distancia radial medida desde el centro de la Tierra,
es la distancia radial medida desde el centro de la Tierra, 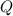 es la carga determinada en el primer apartado y
es la carga determinada en el primer apartado y 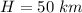 determina la posición de la ionosfera (medida desde la superficie terrestre). Determinar la carga total contenida en la atmósfera terrestre desde la superficie hasta la ionosfera y su signo.
determina la posición de la ionosfera (medida desde la superficie terrestre). Determinar la carga total contenida en la atmósfera terrestre desde la superficie hasta la ionosfera y su signo.
3.Supongamos ahora que la carga de la atmósfera obtenida en el segundo apartado se acumula íntegramente en la ionosfera. Determinar la energía electrostática almacenada por el condensador formado por la superficie de la Tierra y su atmósfera.
4.Para que se produzca un rayo, la diferencia de potencial entre una nube de tormenta y el suelo debe superar el límite de rigidez dieléctrica del aire (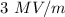 ) a fin de producir una descarga eléctrica que transporta unos
) a fin de producir una descarga eléctrica que transporta unos 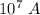 através de un medio ionizado cuya resistencia es de unos
através de un medio ionizado cuya resistencia es de unos 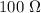 . Estimar la altura máxima de una nube para que pueda ocurrir este fenómeno, y determinar la energía electrostática puesta en juego en el proceso de formación de un rayo de
. Estimar la altura máxima de una nube para que pueda ocurrir este fenómeno, y determinar la energía electrostática puesta en juego en el proceso de formación de un rayo de 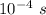 de duración. ¿Cuál sería el mínimo de rayos necesarios para consumir toda la energía del condensador estudiado en el apartado 3?
de duración. ¿Cuál sería el mínimo de rayos necesarios para consumir toda la energía del condensador estudiado en el apartado 3?
Una esfera dieléctrica de radio  está polarizada uniformemente según un vector de polarización
está polarizada uniformemente según un vector de polarización 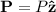 . Determinar el vector
. Determinar el vector 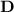 y el vector
y el vector 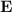 en el centro de la esfera.
en el centro de la esfera.
La filosofía de la resolución del problema consistirá en obtener las densidades de carga ligada e integrar éstas para obtener el campo electrostático, y luego usar la relación entre el desplazamiento eléctrico y la polarización para despejar 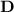 .
.
Tenemos que 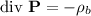 y
y 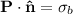 . Como
. Como 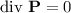 , no hay densidad volumétrica de carga ligada, y en coordenadas esféricas,
, no hay densidad volumétrica de carga ligada, y en coordenadas esféricas, 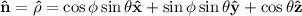 . De esta manera,
. De esta manera, 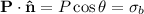 , y tenemos que calcular el campo electrostático debido a esta distribución de carga superficial.
, y tenemos que calcular el campo electrostático debido a esta distribución de carga superficial.
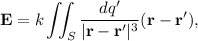
donde 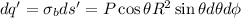 , donde se ha expresado el elemento diferencial de superficie en coordenadas esféricas. Se tiene además que
, donde se ha expresado el elemento diferencial de superficie en coordenadas esféricas. Se tiene además que  (nos interesa el campo en el centro de la esfera) y
(nos interesa el campo en el centro de la esfera) y 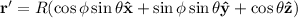 . Sustituyendo tenemos que
. Sustituyendo tenemos que
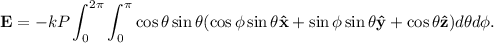
Las integrales en 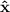 y
y 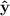 son funciones del tipo
son funciones del tipo 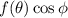 y
y 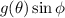 respectivamente, y de esta manera las integrales con respecto a
respectivamente, y de esta manera las integrales con respecto a 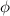 entre
entre 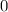 y
y 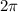 son
son 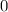 . Por tanto sólo hay campo en
. Por tanto sólo hay campo en 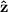 :
:
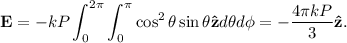
En el SI, 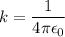 , así que
, así que
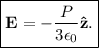
Sabemos además que 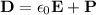 , lo que nos permite concluir que
, lo que nos permite concluir que
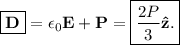
Se puede demostrar además que este es el valor del campo electrostático en toda la esfera dieléctrica (por tanto el vector desplazamiento eléctrico también toma el valor constante calculado en este problema). El lector interesado tiene la demostración en Introduction to Electrodynamics de Griffiths.
Sobre una mesa lisa está sujeta una varilla de longitud 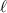 que tiene una carga
que tiene una carga 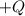 uniformemente distribuida. A una distancia
uniformemente distribuida. A una distancia 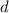 de uno de sus extremos se halla una carga puntual
de uno de sus extremos se halla una carga puntual 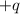 de masa
de masa  . El sistema se esquematiza en la figura.
. El sistema se esquematiza en la figura.
1.Determinar la aceleración inicial de la carga puntual.
2.Obtener la velocidad de la carga puntual cuando ha recorrido una distancia 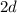 .
.
Determine la capacidad de un condensador formado por dos placas planas de longitud  y anchura
y anchura 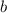 , cuyos planos forman un ángulo
, cuyos planos forman un ángulo 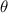 muy pequeño, siendo la distancia mínima que los separa
muy pequeño, siendo la distancia mínima que los separa 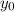 .
.