Problemas de resolución de ecuaciones
La función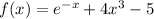 
tiene una raíz en 
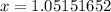. Empezando con 
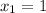y 
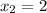, usar ocho iteraciones del método de la bisección para aproximar la raíz. Tabular el error después de cada iteración, y también las estimaciones del error máximo. ¿El error real siempre es menor que la estimación del error máximo? ¿Los errores reales continúan disminuyendo?
De forma general, para hallar una raíz de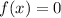 
, dado que 
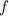es contínua en el intervalo 
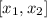, donde el signo de 
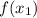es opuesto al signo de 
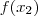, esto es 
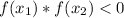, usaremos el siguiente algoritmo del método de la bisección:
A continuación se presenta la tabla con los valores obtenidos para las ocho iteraciones correspondientes:
| Iteración |  |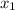
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|
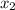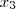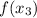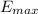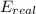| 1 | 1.000000 | 2.000000 | 1.500000 | 8.723130 | 0.500000 | -0.448483 |
| 2 | 1.000000 | 1.500000 | 1.250000 | 3.099005 | 0.250000 | -0.198485 |
| 3 | 1.000000 | 1.250000 | 1.125000 | 3.694997 | 0.125000 | -0.073483 |
| 4 | 1.000000 | 1.125000 | 1.062500 | 0.143442 | 0.062500 | -0.010983 |
| 5 | 1.000000 | 1.062500 | 1.031250 | -0.256598 | 0.031250 | 0.020267 |
| 6 | 1.031250 | 1.062500 | 1.046875 | -0.059688 | 0.015625 | 0.004642 |
| 7 | 1.046875 | 1.062500 | 1.054688 | 0.041094 | 0.007813 | 0.003171 |
| 8 | 1.046875 | 1.054688 | 1.050781 | -0.009492 | 0.003906 | 0.000735 |
Para ocho iteraciones obtenemos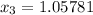 
, que es el valor de 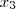más próximo al valor exacto. El error máximo y el error real para cada iteración vienen dados como sigue:
Vemos que el error real es siempre de menor magnitud que el error máximo, es decir, se cumple que:
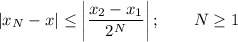
Además, los errores reales disminuyen con cada iteración ya que cada una de ellas es una mejor aproximación que la anterior al valor exacto de la raíz.
Encontrar la raíz cerca 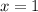de 
de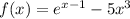 
empezando con 
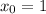. ¿Cuán exacta es la estimación después de cuatro iteraciones del método de Newton? ¿Cuántas iteraciones requiere el método de la bisección para lograr la misma exactitud?. Tabule el número de dígitos correctos en cada iteracción del método de Newton y observe si se duplican cada vez. La solución correcta es x = 0.49404364.
