Problemas de ecuaciones lineales
Este método de Crout se utiliza para resolver sistemas de ecuaciones simultáneas a través de factorización de matrices. Consiste en descomponer la matriz A (matriz de coeficientes de las incógnitas) en dos matrices L y U.

Seguimos los siguientes pasos para la factorización de A:
1a.-
Multiplicamos las filas de L por la primera columna de U e identificamos términos:

y hemos obtenido la que es la primera columna de L.
1b.-
Multiplicamos la primera fila de L por las columnas de U e identificamos términos:
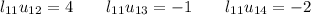
y de esta forma obtenemos la primera fila de U:
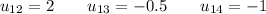
2a.-
Multiplicamos las filas de L por la segunda columna de U e identificamos términos:
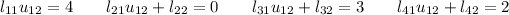
y obtenemos así la segunda columna de L:
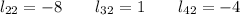
2b.-
Multiplicamos la segunda fila de L por las columnas de U, identificamos términos y obtenemos así la segunda fila de U :
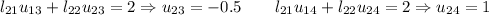
3a.-
Multiplicamos las filas de L por la tercera columna de U, identificamos términos y obtenemos así la tercera columna de L :

3b.-
Multiplicamos la tercera fila de L por las columnas de U, identificamos términos y obtenemos la tercera fila de U:
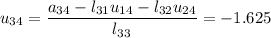
4ab.-
Multiplicamos las filas de L por la cuarta columna de U, identificamos términos y obtenemos la cuarta columna de L :
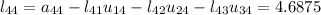
Ya tenemos todos los elementos de ambas matrices, que vienen dadas por:
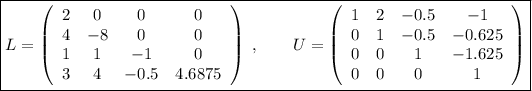
Usando el método de eliminación gaussiana con pivoteo y sustitución regresiva, resuelva el siguiente sistema de ecuaciones:

Calcule el determinante y la descomposición LU de la matriz de coeficientes.



