Problemas de ecuaciones lineales
Usando el método de eliminación gaussiana con pivoteo y sustitución regresiva, resuelva el siguiente sistema de ecuaciones:
Calcule el determinante y la descomposición LU de la matriz de coeficientes.
El método consiste en pasar un sistema de ecuaciones, a uno que pueda ser representado por una matriz triangular superior mediante operaciones elementales entre filas, incluido el pivoteo (intercambio de filas), con el que conseguimos reducir el error por redondeo. Una vez reducida la matriz de los coeficientes, de la ultima ecuación podremos calcular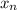 
y a partir de este valor encontrar las demás incógnitas mediante sustitución regresiva:
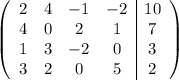
Intercambiamos la primera y segunda fila,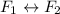 
,
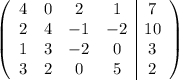
Hacemos las siguientes manipulaciones de filas
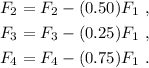
El resultado es
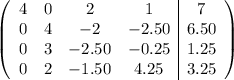
Podemos crear dos ceros más en las dos últimas filas haciendo
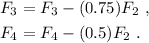
Obtenemos
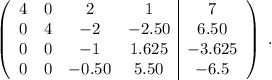
Para terminar de hacer la matriz triangular,
con lo cual
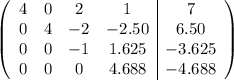
Ahora podemos despejar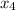 
y por sustitución hacia atrás obtener 
, 
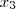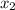y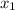 
. El resultado es
Podemos apreciar que la solución obtenida es exacta, aunque en general la solución suele ser una aproximación cercana a la exacta debido al error de redondeo. Sustituyendo en cada paso los ceros por debajo de la diagonal por la razón de coeficientes, tendríamos la matriz ampliada:
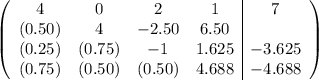
de donde obtenemos la descomposición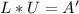 
:
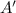es la matriz original permutada debido al pivoteo. Si deshacemos los intercambios de filas realizados, obtenemos la matriz original 
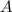de coeficientes. Para hallar el determinante de 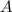, y teniendo en cuenta el intercambio de filas que hemos efectuado. Sea m el número de intercambios de filas, entonces en este caso 
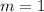y el determinante vendrá dado por:
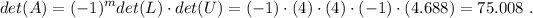
que es muy próximo al valor exacto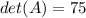 
.
