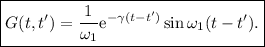Considerando una fuerza constante que actúa tan sólo entre 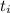 y
y 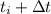 , con
, con 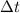 mucho menor que cualquier otra escala de tiempos del problema (con lo cual podemos quedarnos, en cada momento, con el primer orden) obtén la función de Green del oscilador armónico amortiguado, con frecuencia natural
mucho menor que cualquier otra escala de tiempos del problema (con lo cual podemos quedarnos, en cada momento, con el primer orden) obtén la función de Green del oscilador armónico amortiguado, con frecuencia natural 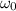 y coeficiente de rozamiento
y coeficiente de rozamiento 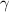 . Considerar los tres casos posibles:
. Considerar los tres casos posibles:
1.oscilador sobreamortiguado,
2.amortiguamiento crítico y
3.oscilador infraamortiguado.
Sin pérdida de generalidad, dado que el método de la función de Green es válido para cualquier conjunto de condiciones iniciales, consideraremos que a 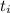 el oscilador está en reposo en la posición de equilibrio.
el oscilador está en reposo en la posición de equilibrio.
La ecuación diferencial del movimiento del oscilador armónico es la siguiente,
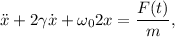
donde 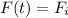 para
para 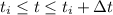 , y
, y 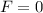 en qualquier otro instante. Como vemos, esto no es más que la preparación para descomponer la fuerza en pequeños intervalos de tiempo donde podemos considerar que es constante.
en qualquier otro instante. Como vemos, esto no es más que la preparación para descomponer la fuerza en pequeños intervalos de tiempo donde podemos considerar que es constante.
La posición en el instante final se puede obtener sencillamente integrando la velocidad,
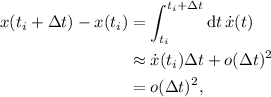
donde en el último paso hemos tenido en cuenta las condiciones iniciales de reposo en equilibrio. Procediendo de forma similar, podemos obtener la velocidad en el instante final del intérvalo,
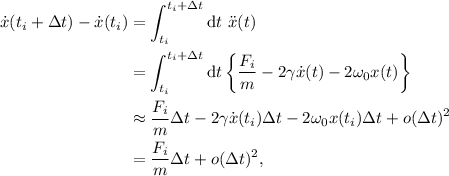
donde, en el primer paso, hemos tenido en cuenta la ecuación diferencial del oscilador, ec. (1).
Los valores obtenidos no son más que las condiciones iniciales para el movimiento del oscilador a partir de 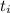 . A partir de ese momento, el oscilador se moverá según el tipo de amortiguamiento siguiendo las soluciones generales, que se pueden consultar en el diccionario de ecuaciones. Por lo tanto, tenemos que distinguir entre los tres casos.
. A partir de ese momento, el oscilador se moverá según el tipo de amortiguamiento siguiendo las soluciones generales, que se pueden consultar en el diccionario de ecuaciones. Por lo tanto, tenemos que distinguir entre los tres casos.
En este caso, la solución general es de la forma
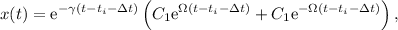
donde 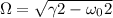 . Las constantes
. Las constantes 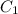 y
y 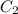 se obtienen imponiendo las condiciones iniciales (2) y (3). El resultado es
se obtienen imponiendo las condiciones iniciales (2) y (3). El resultado es
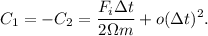
Así, pues, tenemos
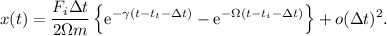
Desarrollando por Taylor las exponenciales vemos como los términos lineales en 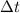 se cancelan entre si, y los órdenes más elevados se ajuntan con el
se cancelan entre si, y los órdenes más elevados se ajuntan con el 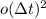 . Con los términos restantes, podemos reconstruir las exponenciales, quedandonos
. Con los términos restantes, podemos reconstruir las exponenciales, quedandonos
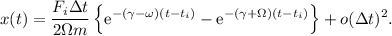
Llegados a este punto, observamos que el coeficiente que multiplica a la ecuación proviene de considerar la fuerza constante en un intervalo de tiempo único. Si consideramos diferentes intervalos con diferentes valores de la fuerza 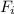 , reconstruimos la dependencia general de una fuerza general
, reconstruimos la dependencia general de una fuerza general 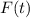 . En este caso, gracias al principio de superposición, podemos considerar una solución particular del tipo (7) para cada intervalo de tiempo, con lo cual la solución total es una superposición (suma) de todas las soluciones particulares,
. En este caso, gracias al principio de superposición, podemos considerar una solución particular del tipo (7) para cada intervalo de tiempo, con lo cual la solución total es una superposición (suma) de todas las soluciones particulares,
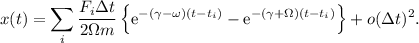
Si tomamos el límite  , reconocemos la definción de la integral de Riemann,
, reconocemos la definción de la integral de Riemann,
La función de Green es todo aquello que acompaña, en el integrando, al término inomohéneo de la ecuación diferencial (1), por tanto
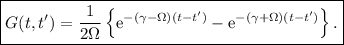
En este caso, 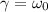 y las soluciones son de la forma
y las soluciones son de la forma
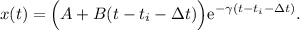
Las condiciones iniciales (2) y (3) determinan
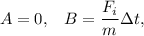
con lo cual, la solución final, una vez realizado el sumatorio para todos los diferentes intervalos de tiempo, siguiendo el mismo razonamiento que en el caso anterior, es
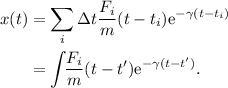
así, pues, tenemos
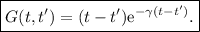
Este caso se obtiene directamente del caso sobreamortiguado simplemente realizando la substitución 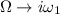 , donde
, donde 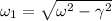 . Por tanto, el resultado final es
. Por tanto, el resultado final es
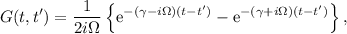
O bien, escrito de otra forma,