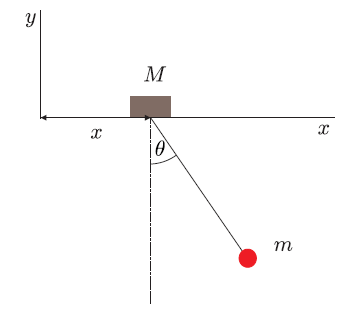
Considere el sistema formado por la masa 
que puede deslizar libremente sobre una recta horizontal, y 
unida mediante una varilla rígida y sin masa a M,pudiendo girar libremente en un plano vertical.
1.Obtenga la Lagrangiana de este sistema.
2.Determine las integrales primeras de movimiento.
3.Suponga ahora que se impone una velocidad constante 
a y discuta la existencia de integrales primeras.
Las posiciones de cada una serán:
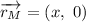
De :
De :
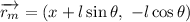
Derivando:
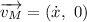
y
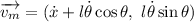
Las energías serán:
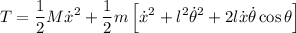
y
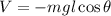
Luego
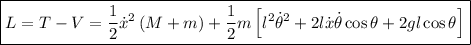
Las integrales primeras de movimiento las podremos saber a la vista de la forma funcional del lagrangiano, pues no es función de 
, i.e. es una coordenada cíclica por lo que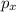 
es una integral primera de movimiento.
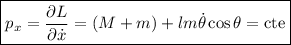
Además, como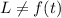 
, 
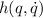es constante y como el potencial no es función de las velocidades generalizadas la integral de Jacobi coincide con la energía mecánica del sistema, por lo que
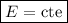
es otra integral primera de movimiento
(Se podría probar también a partir d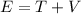e 
que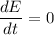 
).
Ahora, si el soporte () se mueve a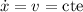 
, el Lagrangiano quedaría:
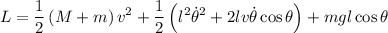
En este caso, la única coordenada generalizada es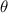 
y no es cíclica luego no hay momento generalizado constante.
El lagrangiano sigue sin ser función del tiempo y el potencial sigue sin ser función de las velocidades generalizadas, luego el Hamiltoniano es constante. Pero como la energía cinética no es una función cuadrática de las velocidades generalizadas el hamiltoniano no coincide con la energía.
