Un punto de masa  se mueve por una trayectoria rectilínea bajo la acción de una fuerza proporcional al tiempo (el coeficiente de proporcionalidad es
se mueve por una trayectoria rectilínea bajo la acción de una fuerza proporcional al tiempo (el coeficiente de proporcionalidad es 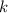 ). Además, el punto experimenta por parte del medio una resistencia viscosa por parte del aire proporcional a la velocidad (el coeficiente de proporcionalidad es
). Además, el punto experimenta por parte del medio una resistencia viscosa por parte del aire proporcional a la velocidad (el coeficiente de proporcionalidad es 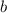 ). En el instante inicial la velocidad es igual a cero.
). En el instante inicial la velocidad es igual a cero.
1.Encuentre la evolución de la velocidad respecto del tiempo en el caso en que no hay resistencia del aire (es decir, cuando 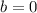 ).
).
2.Resuelva el problema en el caso general, con 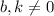 .
.
3.Compruebe que el resultado del segundo apartado se reduce al del primero tomando el límite 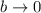 .
.
Si no actúa la fricción viscosa, la segunda ley de Newton se convierte en la siguiente ecuación diferencial,
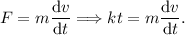
Esta es una ecuación diferencial separable, que se puede resolver con la manipulación formal de los diferenciales,
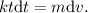
Finalmente, podemos integrar entre el momento inicial (en que el tiempo y la velocidad son ambos 0) y un instante genérico en que el tiempo es t y la velocidad v(t),
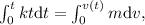
lo que nos da
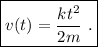
La aparición de la fuerza de fricción viscosa se traduce en un nuevo término en nuestra ecuación diferencial. Comoquiera que la fuerza de fricción siempre es opuesta al movimiento, entonces dicho término siempre tendrá signo opuesto a la velocidad. Por lo tanto, el término adicional tomará la forma 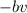 . Con lo cual, la ecuación diferencial a resolver es
. Con lo cual, la ecuación diferencial a resolver es
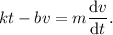
Ya no tenemos una ecuación separable. No obstante, no se trata de una ecuación mucho más difícil, ya que reorganizando los términos,
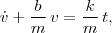
reconocemos una ecuación diferencial de primer grado lineal con coeficientes constantes y un término inhomogéneo. Recordad que el punto señala la derivación respecto del tiempo. La solución de este tipo de ecuaciones se puede hallar a partir de la solución general de la ecuación homogénea (es decir, retirando todos los términos que dependan de t de forma explícita) más una solución particular de la ecuación completa.
La ecuación homogénea es
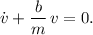
Esta ecuación puede resolverse por el método habitual de ensayar una solución del tipo 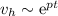 , o bien dándonos cuenta de que esta sí es una ecuación separable. Mediante cualquiera de los métodos, el resultado es
, o bien dándonos cuenta de que esta sí es una ecuación separable. Mediante cualquiera de los métodos, el resultado es
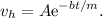
Para encontrar una solución particular a la ecuación (5) podemos inspirarnos en el hecho de que el término inhomogéneo es polinomial. En estos casos, conviene ensayar una solución también polinomial del mismo grado. Es decir, probamos una solución del estilo 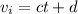 . Una solución de este estilo arroja la siguiente ecuación,
. Una solución de este estilo arroja la siguiente ecuación,
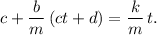
Dicha ecuación debe ser válida para cualquier instante de tiempo. Por lo tanto, los coeficientes de cada término del polinomio deben satisfacer la ecuación, lo cual nos permite obtener dos ecuaciones,
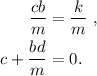
\end{aligned}
De la primera ecuación obtenemos 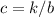 . Substituyendo este resultado en la otra ecuación obtenemos
. Substituyendo este resultado en la otra ecuación obtenemos
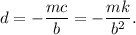
Por lo tanto, la solución particular es
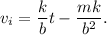
Juntando todas las piezas, la solución general de la ecuación competa (5) es
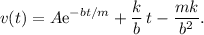
Esta solución está sometida a la condición inicial 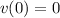 , lo cual implica
, lo cual implica 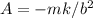 . Con esto, el resultado final es
. Con esto, el resultado final es
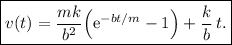
Este último apartado nos invita a analizar el comportamiento asintótico de la solución (13) cuando 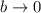 . Vemos que una aplicación ingenua del límite no es muy prometedora, ya que
. Vemos que una aplicación ingenua del límite no es muy prometedora, ya que 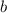 aparece en el denominador de diversas fracciones. En estos casos, la forma más prometedora de proceder es realizar una expansión de Taylor. En nuestro caso, necesitamos la expansión de la exponencial,
aparece en el denominador de diversas fracciones. En estos casos, la forma más prometedora de proceder es realizar una expansión de Taylor. En nuestro caso, necesitamos la expansión de la exponencial,
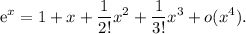
En nuestro caso tenemos
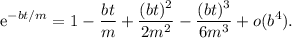
Insertando este resultado en (13) obtenemos
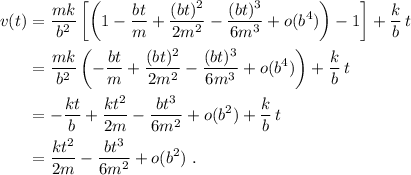
Tan sólo el primer término sobrevive cuando 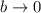 , por lo que tenemos
, por lo que tenemos
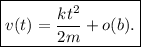
Efectivamente, el resultado es coherente con el que obtuvimos en (3). Nótese que hemos necesitado mantener los tres primeros términos del desarrollo de Taylor, ya que los dos primeros se anulaban en el resultado final. Si hubiéramos mantenido menos términos de los necesarios, hubiéramos obtenido cero como resultado final. Como norma general, si tras aplicar un desarrollo de Taylor nos sale cero, normalmente significa que debemos mantener más términos del desarrollo. En nuestro caso concreto, el hecho de que hubiera un coeficiente con una potencia 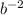 era un claro indicador de que íbamos a necesitar expandir hasta, por lo menos,
era un claro indicador de que íbamos a necesitar expandir hasta, por lo menos, 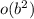 . Por otra parte, nunca está de más mantener un término extra que será desechado al final (como hemos hecho esta vez).
. Por otra parte, nunca está de más mantener un término extra que será desechado al final (como hemos hecho esta vez).


