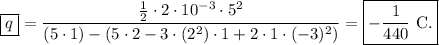En cierta región del espacio, el potencial eléctrico viene dado por
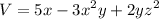
en unidades SI.
1.Calcule las expresiones de las componentes 
, 
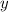y 
del campo eléctrico en dicha región del espacio.
2.¿Cuál es el módulo del campo en el punto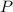 
de coordenadas 
?
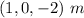3.El punto 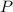y el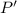 
de coordenadas 
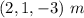están unidos por un conducto rígido, por el que se puede mover, sin rozamiento, una esfera pequeña de 
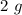, que tiene una carga 
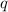desconocida. Cuando se abandona en reposo dicha esfera en el punto 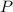, se observa que llega a 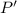con una velocidad de 
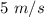. ¿Cuál es el signo de la carga?, ¿y su valor? No considere el campo gravitatorio.
Sólo tenemos que tener en cuenta que 
, es decir
o sea
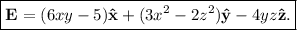
Tenemos que
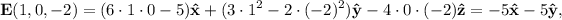
y tenemos simplemente que
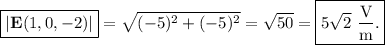
En este apartado podemos usar el principio de conservación de la energía mecánica, ya que la única interacción que interviene es la electrostática, que es conservativa. Entonces
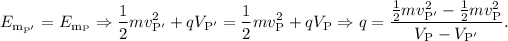
Sabemos que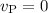 
, 
, 
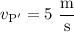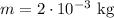, y los potenciales se calculan simplemente sustituyendo en la fórmula del enunciado. Por tanto
