Un disco uniforme de masa 
, radio 
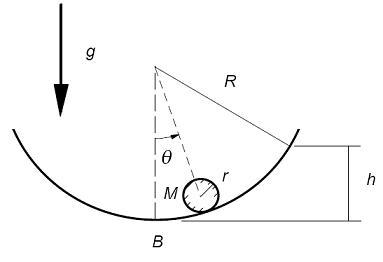
y espesor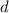 
rueda sin resbalar sobre una superficie esférica de radio 
como se muestra en la figura. El movimiento es plano.
1.Encontrar el tiempo para el cuál el radio vector que une el centro del hemisferio esférico con el centro del disco barre un ángulo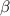 
.
2.Encontrar el periodo para el caso en que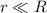 
.
Teniendo en cuenta que el cuerpo realiza su movimiento debido al peso que posee (a una de sus componentes del peso), se conserva la energía mecánica del sistema.
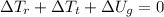
Donde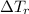 
es la variación de energía rotacional, 
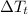es la variación de energía de translación y 
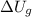es la variación de energía potencial gravitatoria
Entonces:
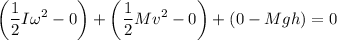
Dond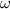e: 
, 
e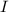 
son la rapidez angular, rapidez lineal y momento de inercia del disco respectivamente.
Y teniendo en cuenta que para un disco su momento de inercia está dado por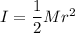 
y como el disco no resbala vale que 
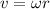y además de la figura 
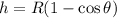entonces:
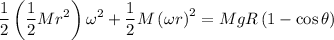
Resolviendo se tiene que:
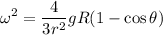
Luego considerando que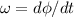 
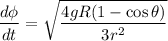
Y además notando que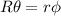 
, 
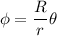(esto debido a que la longitud de arco barrida por el cilindro es la misma longitud que recorre de un punto a otro sobre la superficie esférica), 
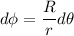la expresión anterior puede escribirse como:
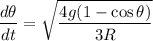
Entonces:
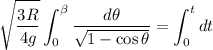
Por lo tanto:
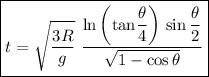
Partiendo de que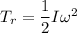 
y teniendo en cuenta la ec. (4) se obtiene:
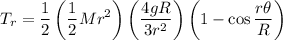
Luego considerando que el torque sobre al disco vine dado por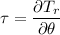 
entonces de la ec. (9) se tiene que:
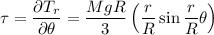
Pero como por condición del problema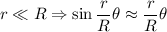 
, por lo tanto se tiene que:
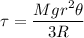
Además tomando en cuenta que la ecuación de la dinámica de rotación esta dada por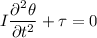 
se tiene que:
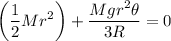
Esta última expresión obtenida no viene a ser otra que la ecuación de un MAS y su periodo esta dado por:
Como se puede apreciar el periodo no depende del radio del disco si no solamente del radio de la superficie esférica donde se realiza la oscilación.
