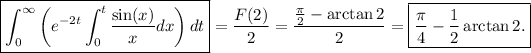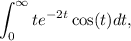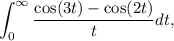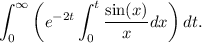Problemas de transformadas integrales
Esta integral se puede evaluar integrando por partes y aplicando la regla de Barrow, tomando límites para el límite superior. Este cálculo es ciertamente tedioso (la integral indefinida resulta ser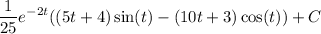 
), así que vamos a aprovechar las propiedades de la transformada de Laplace para calcular el valor de la integral.
En primer lugar, debemos recordar que tal transformada integral se define como
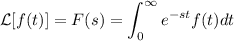
para los valores de 
donde la integral converge. A la vista de la integral, podemos afirmar que 
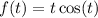, y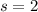 
. Debemos encontrar pues, mediante propiedades sencillas, la transformada de 
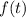y evaluarla en 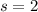. Sabemos que
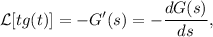
donde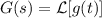 
. En el caso que nos ocupa, 
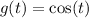, y sabemos que (por integración o consultando una tabla de transformadas)
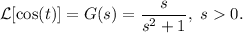
Derivando con respecto a y cambiando el signo, tenemos que
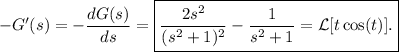
Particularizando en 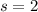se tiene que
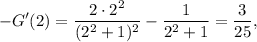
luego
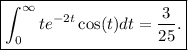
Haremos uso de la misma estrategia, siendo más fructífera en este caso la utilización de transformadas de Laplace ya que ahora la primitiva, lejos de ser de difícil obtención, ni es expresable en términos de funciones elementales. Recordemos que
donde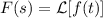 
. Esta propiedad es válida si se cumplen algunas hipótesis, entre las cuales tenemos que debe existir y ser finito el siguiente límite:
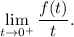
En efecto
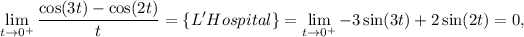
entonces
con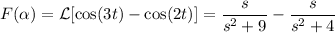 
, es decir
A la vista del integrando, haciendo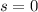 
debemos recuperar el valor de la integral pedida:
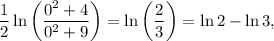
y
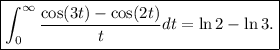
De nuevo nos vemos obligados a recurrir a la transformada de Laplace, pues la integral interior no posee expresión analítica en forma cerrada (closed-form), que es lo que pasaba en el caso anterior. Calcularemos la transformada de Laplace de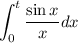 
y particularizaremos en .
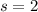Sabemos que
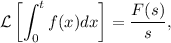
donde 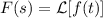. Tenemos que
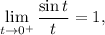
luego
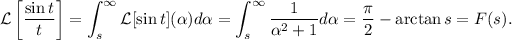
De esta manera
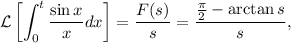
con lo que
