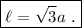Problemas de ondas mecánicas
Nivel: Primer ciclo
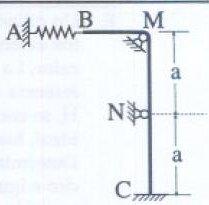
La cuerda BC de la figura es homogénea, e inextensible, que cambia de dirección en M mediante un apoyo liso de dimensiones despreciables, y está unida a un muelle AB sin deformar. La cuerda se tensa desplazando un segundo apoyo N, también liso, según la línea discontinua equidistante a M y C representada en la figura. Determinar el desplazamiento de N que hace máximas las frecuencias de vibración estacionarias en los segmentos MN y NC.
Al mover N una distancia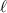 
, se incrementará la distancia MN (y NC, que será la misma), según el teorema de Pitagoras,
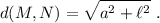
Naturalmente, la distancia MN será mayor a 
. Como la cuerda es inextensible, esa longitud tiene que venir de la parte horizontal de la cuerda. Por lo tanto, el muelle se tendrá que estirar una distancia
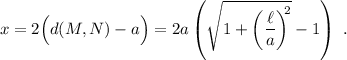
El factor dos viene de tener en cuenta que en el segmento NC pasa lo mismo. Según la ley de Hooke, el muelle proporciona una fuerza proporcional a esa elongación,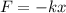 
. Esa fuerza será igual a la tensión de la cuerda, que determina la velocidad de las ondas en la cuerda,
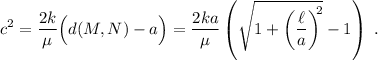
En el estado fundamental de las ondas estacionaras, sólo habrá un vientre entre los puntos M y N. Por lo tanto, la longitud de onda será igual al doble de la distancia entre ambos puntos,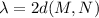 
.
La frecuencia de vibración depende de velocidad y longitud de onda,
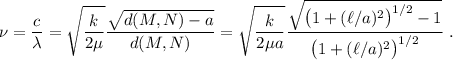
Ahora simplemente se trata de buscar el máximo de esta función. Para ello, simplemente derivamos,
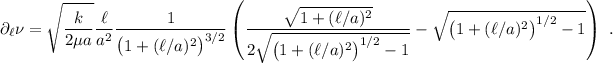
Parece complicado, pero no lo es tanto. Al igualar a cero, todos los factores fuera del paréntesis cancelan, y nos queda la ecuación
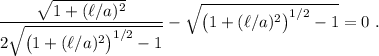
Si multiplicamos por el denominador,
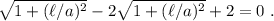
Con lo que nos queda
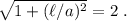
Por último, elevando al cuadrado y aislando tenemos
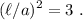
Es decir,
