Problemas de leyes de newton en una dimensión
Nivel: Secundaria
Si al aplicar una fuerza a un cuerpo aparece una reacción igual y de sentido contrario, ¿cómo es posible que lo ponga en movimiento?
Un trabajador debe lanzar un paquete de 5kg desde el suelo hasta una altura de 4m. Si el trabajador aplica al paquete una fuerza vertical constante desde el suelo hasta que encuentra a una altura de 1,5m, calcula:
1.el módulo de la fuerza mínima necesaria para que el paquete alcance los 4 m.
2.en estas condiciones, tiempo total empleado en subir el paquete.
Para empezar debemos considerar que el problema está dividido en dos partes. La primera sería des de que el trabajador coge el paquete hasta que lo suelta. La segunda parte sería des de que suelta el paquete hasta que llega a los 4 metros.
Para empezar, sabemos que la fuerza que debe hacer el trabajador depende de la masa del paquete y de la aceleración que va a necesitar. Como ya conocemos la masa (m), vamos a calcular la aceleración (a): La aceleración total será la producida por el obrero ([ERROR DE LaTeX. Error: 4 ]) menos la aceleración de la gravedad ([ERROR DE LaTeX. Error: 4 ]). Entonces, como la aceleración total debe producir una velocidad final que permita al cuerpo ascender hasta los 4m, vamos a calcular cual es esa velocidad final: si sabemos que...
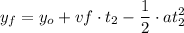
Conocemos la y final, la y inicial, la velocidad final y la aceleración, que es la gravedad. Solo nos falta el tiempo (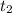 ).
).
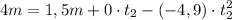
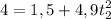
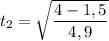
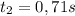
Vale, ahora que conocemos el tiempo que tarda en llegar a los 4 metros (des de que se suelta el paquete), podemos calcular cual era la velocidad inicial con 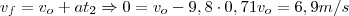 Ya sabemos que la aceleración que producirá el trabajador va a provocar que el paquete acelere hasta llegar a los 6,9m/s, de esta manera ya lo sabemos casi todo, conocemos la "y" final (en el lanzamiento, 1,5m) la "y" inicial (0m), la velocidad inicial y la final, solo nos falta la aceleración producida y el tiempo (
Ya sabemos que la aceleración que producirá el trabajador va a provocar que el paquete acelere hasta llegar a los 6,9m/s, de esta manera ya lo sabemos casi todo, conocemos la "y" final (en el lanzamiento, 1,5m) la "y" inicial (0m), la velocidad inicial y la final, solo nos falta la aceleración producida y el tiempo (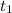 ) que tarda el obrero en lanzar el cuerpo. Como expresamos esto? Pues así:
) que tarda el obrero en lanzar el cuerpo. Como expresamos esto? Pues así:
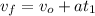
Entonces,
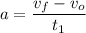
Por otro lado...
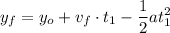
Substituimos "a" de (7) y la colocamos en (8),
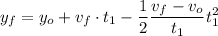
Calculamos
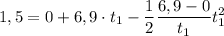
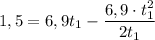
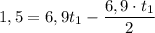
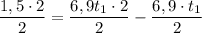
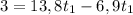
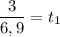
Pues ya conocemos el tiempo, ahora la aceleración será:
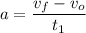
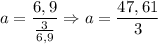
Conociendo la aceleración, la fuerza es cosa fácil, con la segunda ley de Newton (F=ma)
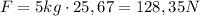
I el tiempo va a ser el de "lanzamiento" más el de subida,
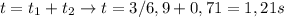
Una persona está sobre una balanza dentro de un ascensor que sube con aceleración 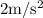 (aceleración y velocidad del ascensor apuntan hacia arriba). Si la masa de la persona es 89kg, encontrar el peso (aparente) que marca la balanza en esta situación.
(aceleración y velocidad del ascensor apuntan hacia arriba). Si la masa de la persona es 89kg, encontrar el peso (aparente) que marca la balanza en esta situación.
Tres bloques A, B y C (de masas 1, 2 y 3 kg, respectivamente) se encuentran sobre una superficie horizontal como se indica en la figura siguiente.
1.¿Qué fuerza hay que aplicarle a C para que los bloques adquieran una 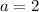 m/s
m/s ?
?
2.Fuerza que ejerce A sobre B.
3.Fuerza que ejerce B sobre C.
4.Repetir el problema si suponemos que la fuerza se aplica sobre A (hacia la derecha).
El coeficiente de fricción estática entre el piso de un camión y una caja que descansa sobre el es de 0,30. La velocidad del camión es de 22.22m/s. ¿Cual es la distancia mínima de frenado del camión para que la caja no se deslice?
Un cuerpo de masa 2 kg desciende en caída libre. Toma 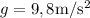 .
.
1.¿Qué fuerza constante es necesario aplicarle en el instante en que su velocidad es de 20,4 m/s para detenerlo en 2 s?
2.¿Qué trabajo se realiza sobre el cuerpo desde que se aplica la fuerza hasta que se detiene?
Tenemos una jaula de 1kg de peso, y un pájaro en su interior que pesa 10g. Si el pájaro no se posa en la jaula, sino que permanece revoloteando, ¿cuánto pesará el conjunto de la jaula y el pájaro si la jaula es hermética? ¿y si es de barrotes?



