Problemas de movimiento en más de una dimensión
Nivel: Secundaria
Razonar si son verdaderas o falsas las siguientes afirmaciones:
1.El vector velocidad es siempre tangente a la trayectoria.
2.Los vectores velocidad y aceleración tienen siempre la misma dirección.
3.El vector velocidad puede variar de dirección sin variar su módulo.
4.A veces el vector velocidad tiene sentido opuesto al vector aceleración.
¿Puede variar la dirección de la velocidad de un objeto mientras su aceleración es constante en módulo y dirección?
Desde lo alto de una torre de 200m de altura se dispara un proyectil con una velocidad inicial de 60m/s, formando un ángulo de 60º con la horizontal. Calcular:
1.El módulo de la velocidad cuando llega al suelo.
2.Alcance total.
Apartado 1
Estamos ante un tiro parabólico completo,resultante de uno de avance horizontal, rectilíneo y uniforme, y otro rectilí- neo y uniformemente acelerado; por tanto las ecuaciones según OX serán:
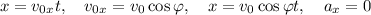
La aceleración en este caso es cero, de ahí que sea un movimiento uniforme. Por otro lado, las ecuaciones del movimiento en el eje OY son:
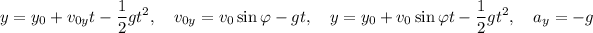
Por tanto, las ecuaciones del movimiento del cuerpo serán:
[ERROR DE LaTeX. Error: 4 ]
[ERROR DE LaTeX. Error: 4 ]
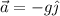
Cuando el cuerpo alcanza el suelo, 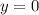 luego:
luego:
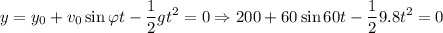
Tras resolver la ecuación de segundo grado, se obtienen dos valores para el tiempo:
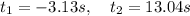
El tiempo que tarda en alcanzar el suelo es por tanto 13.04s aproximadamente, ya que la segunda solución de la ecuación cuadrática no tiene significado físico. Por tanto, la velocidad con la que llega al suelo es:

Apartado 2
En lo que respecta al alcance total, es la distancia desde el lugar en el que se lanzó el cuerpo al punto en que el cuerpo pasa por la misma horizontal de aquél. En realidad ya lo hemos hemos hecho, al hacer que 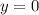 . De todos modos, hay una expresión para calcular el alcance total a la que podemos llegar de la siguiente forma:
. De todos modos, hay una expresión para calcular el alcance total a la que podemos llegar de la siguiente forma:
En la ecuación del movimiento, despejamos el tiempo, teniendo en cueta que hay una altura inicial:
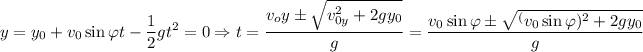
Para hallar el alcance máximo o total, simplemente multiplicamos este valor por:
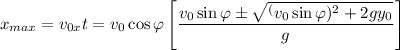
El resultado al que se llega es el siguiente:
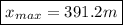
Lógicamente tomando el valor del tiempo con significado físico, es decir, no el valor negativo.
Un centrocampista trata de sorprender desde 50m de la portería a un portero adelantado golpeando en la dirección correcta el balón, que sale de su bota a 80Km/h y con un ángulo de 45º del suelo. El portero se encuentra a 7 metros de su portería y tarda 1s en reaccionar y retroceder a una velocidad de 2m/s. Teniendo en cuenta que la altura de la portería es de 2,10m. ¿Será gol o no?
Un avión vuela horizontalmente a una altura de 1,2 km con una velocidad de 180 km/h.
a) ¿Cuánto tiempo antes de que el avión esté sobre el blanco debe dejar caer la bomba? b) ¿Cuál es la velocidad de la bomba al llegar al suelo? c) ¿Cuál es la velocidad de la bomba 10 s después de ser soltada? d) ¿Cuál es la velocidad de la bomba cuando se encuentra a 200 m de altura? e) ¿Cuál es el ángulo que forma con el eje horizontal la velocidad de la bomba al caer al suelo? f) ¿Cuál es la distancia horizontal cubierta por la bomba?
na partícula está animada de una velocidad de componentes:
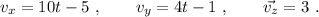
Si su vector posición para 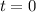 es
es 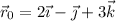 , calcula:
, calcula:
1.Aceleración a los 3 s.
2.Desplazamiento entre 2 y 3 s.
3.Componentes intrínsecas de la aceleración.
Se lanza horizontalmente una pelota con una velocidad de 2 m/s desde una altura de 20 m sobre el suelo. Despreciando la resistencia del aire y tomando como origen el punto del suelo situado en la vertical del punto de lanzamiento, calcular:
1.Su posición después de 1 s.
2.Tiempo que tarda en llegar al suelo.
3.Velocidad en ese instante.
En un hipotético origen de coordenadas se lanza verticalmente hacia arriba una pelota con una velocidad inicial de 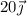 m/s. Sobre la pelota, de peso P, el viento ejerce una fuerza
m/s. Sobre la pelota, de peso P, el viento ejerce una fuerza 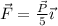 (N).
Calcular:
(N).
Calcular:
1.los vectores velocidad y posición en el punto más alto de su trayectoria.
2.los vectores velocidad y posición en el momento de llegar al suelo.
Al romperse la cuerda que sujeta dos partículas A y B, el resorte comprimido hace que las partículas se separen . La energía potencial del resorte comprimido es de 27,12 J, y el conjunto inicialmente tiene una velocidad 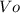 =6,096 m/s en la dirección en que se indica en la figura. Si la cuerda se rompe cuando
=6,096 m/s en la dirección en que se indica en la figura. Si la cuerda se rompe cuando 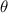 = 30°:
= 30°:
a) determinar la velocidad final de cada partícula. cuando el resorte no esta unido a las partículas
b) Si la constante del resorte es k y los extremos del mismo estan unidos a cada partícula describa con ecuaciones el movimiento subsecuente de las mismas.
Peso de A= 8,89 N Peso de B= 13,34 N
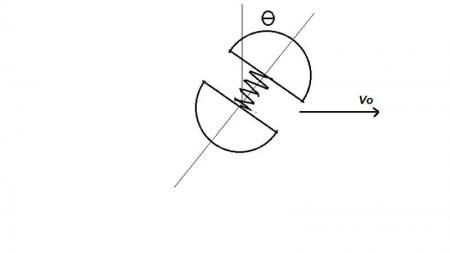
Figura 1. La de arriba es B y la particula de abajo es A (Haz click para ver la imagen a tamaño real)
Considere la gravedad actuando en dirección perpendicular al esquema.
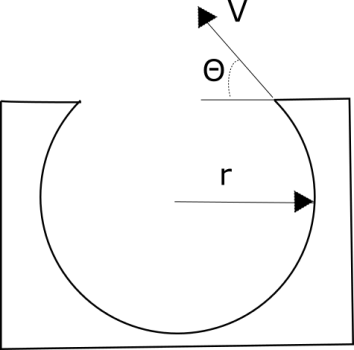
Un skater de 70 kg ha decidido probar al límite la nueva pista del parque, la forma característica cilíndrica tiene un radio de 2.5 m, el sabe que al momento de entrar en la pista por la horizontal debe desarrollar una velocidad de 8 m/s para lograr hacer el salto de un extremo de la pista al otro
1.Cual es el ángulo 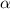 de la con que fue diseñada la pista.
de la con que fue diseñada la pista.
2.Cual es la altura máxima de vuelo.
3.Cuanto tiempo esta en aire hasta aterrizar sobre la pista.
Las posiciones que ocupa un móvil vienen indicadas por las ecuaciones siguientes (donde todas las magnitudes están expresadas en el S.I.):
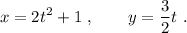
Halla, para el instante 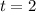 s:
s:
1.Posición del móvil.
2.Vector velocidad y su módulo.
3.Aceleración.
4.Sus componentes intrínsecas.
5.Radio de curvatura.
6.Clase de movimiento
7.Velocidad y aceleración medias entre 2 y 3 s.
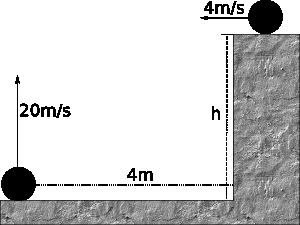
Se lanza un objeto verticalmente hacia arriba con una velocidad 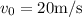 . Al mismo tiempo, y desde una altura h, se lanza horizontalmente, tal como se muestra en la figura 1, otro objeto con una velocidad
. Al mismo tiempo, y desde una altura h, se lanza horizontalmente, tal como se muestra en la figura 1, otro objeto con una velocidad 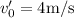 . Si la distancia horizontal que separaba inicialmente los dos objetos era de 4m, determinar:
. Si la distancia horizontal que separaba inicialmente los dos objetos era de 4m, determinar:
1.El valor de h necesario para que los dos objetos se encuentren.
2.El tiempo que transcurre hasta que se encuentran
Durante una de sus peripecias, McGiver tiene que saltar de un vagón en marcha. ¿Cómo lo haría para hacerse el menor daño posible?
Una fuerza dependiente del tiempo 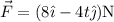 , (donde t está en segundos), se aplica a un objeto de 2kg inicialmente en reposo.
, (donde t está en segundos), se aplica a un objeto de 2kg inicialmente en reposo.
1.¿En qué tiempo el objeto se moverá con una velocidad de 15 m/s?
2.¿A qué distancia está de su posición inicial cuando su velocidad es 15 m/s?
3.¿Cuál es la distancia total recorrida por el objeto en este instante?