Problemas de movimiento circular
Nivel: Secundaria
Un móvil recorre una trayectoria circular con módulo de la velocidad constante. El momento angular de la partícula móvil respecto al centro de la trayectoria
- es nulo.
- cambia con el tiempo.
- tiene el módulo constante, mas no su dirección.
- es constante.
Solución: d.
Recordemos que el momento angular de una partícula es 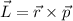 , donde
, donde 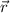 es el vector de posición de la partícula, tomando su origen en el punto respecto del cual hacemos el cálculo del momento angular (el centro de la trayectoria en este ejercicio) y
es el vector de posición de la partícula, tomando su origen en el punto respecto del cual hacemos el cálculo del momento angular (el centro de la trayectoria en este ejercicio) y 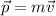 el momento lineal de la partícula.
el momento lineal de la partícula.
Como en cualquier producto vectorial, el resultado es un vector perpendicular a ambos operandos. Puesto que ambos vectores, 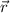 y
y 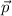 , están en este ejercicio confinados en el plano de la trayectoria, es obvia la constancia de la dirección de
, están en este ejercicio confinados en el plano de la trayectoria, es obvia la constancia de la dirección de 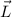 , perpendicular a dicho plano.
, perpendicular a dicho plano.
También es evidente la constancia del sentido de 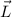 , pues los vectores
, pues los vectores 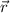 y
y 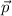 mantienen, en este caso, su orientación relativa.
mantienen, en este caso, su orientación relativa.
Por último, como dichos vectores forman entre sí un ángulo de 90º, el módulo de 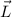 será [ERROR DE LaTeX. Error: 4 ]. Puesto que en este movimiento tanto
será [ERROR DE LaTeX. Error: 4 ]. Puesto que en este movimiento tanto  , como
, como  , como
, como  son constantes, también concluimos que el módulo del momento angular se mantiene constante.
son constantes, también concluimos que el módulo del momento angular se mantiene constante.


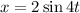 ,
, 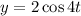 obtener la clase de movimiento y la ecuación de la trayectoria.
obtener la clase de movimiento y la ecuación de la trayectoria.