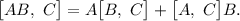Problemas de mecánica cuántica
Un oscilador armónico se encuentra inicialmente en el estado
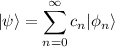
en donde 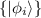 son los vectores propios del hamiltoniano.
Demuestra que el valor medio de la posición evoluciona con el tiempo de acuerdo a
son los vectores propios del hamiltoniano.
Demuestra que el valor medio de la posición evoluciona con el tiempo de acuerdo a
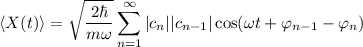
siendo 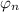 la fase de
la fase de 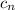 .
.
Primero, adelantamos que en la resolución se usará por comodidad el convenio de suma sobre índices repetidos de Einstein.
Dado que las soluciones para la energía son de la forma 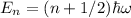 , el ket de nuestro estado tendrá por componentes (es decir, en la base de vectores propios del hamiltoniano será de la forma):
, el ket de nuestro estado tendrá por componentes (es decir, en la base de vectores propios del hamiltoniano será de la forma):
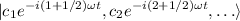
o de forma sintetizada, serán todos de la forma
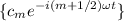
y su bra correspondiente será pues de la forma 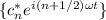
Debemos realizar pues la operación
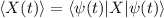
Para ello, obtengamos la matriz de posición. Por definición:
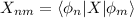
Ahora bien, dado que el operador posición lo podemos escribir como 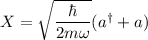 , donde
, donde 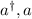 son los operadores de creacción y aniquilación respectivamente, y además sabemos que estos actúan sobre los vectores de la base como sigue:
son los operadores de creacción y aniquilación respectivamente, y además sabemos que estos actúan sobre los vectores de la base como sigue:
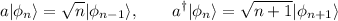
y la base de vectores propios del hamiltoniano es ortonormal, se demuestra que la expresión matricial del operador posición es:
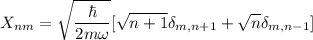
con lo que la ecuación (3) queda
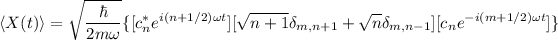
donde recordemos se está usando el convenio de suma de Einstein. Ahora desarrollemos la expresión: fijémonos en que una delta nos hará colapsar 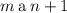 y la otra a
y la otra a  , por lo que se puede reescribir el producto de los dos primeros corchetes como:
, por lo que se puede reescribir el producto de los dos primeros corchetes como:
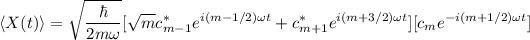
Ahora ya, por comodidad visual podemos volver a escribir sumatorios, cambiando el comienzo de la suma de m=0 a m=1 y reescribiendo consecuentemente los índices. Tenemos pues una expresión para el valor esperado del operador posición de la forma:
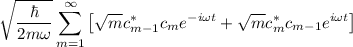
Pero en la expresión que buscamos aparecen los módulos de las componentes, por lo que hacemos 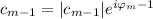 y
y 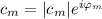 y, dado que al hacerlo sale factor común
y, dado que al hacerlo sale factor común 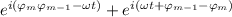 lo que es igual a
lo que es igual a 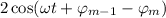 obtenemos el resultado requerido:
obtenemos el resultado requerido: