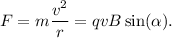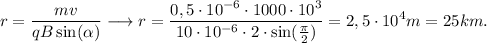Problemas de campo magnético estático
Un electrón se mueve en el eje positivo de las x, con una velocidad de  . Entra a una región cuya campo magnético es 0.8T en la dirección positiva del eje de la z. ¿Cuál será la magnitud y dirección de la fuerza magnética que experimenta el electrón? Hazlo:
. Entra a una región cuya campo magnético es 0.8T en la dirección positiva del eje de la z. ¿Cuál será la magnitud y dirección de la fuerza magnética que experimenta el electrón? Hazlo:
1.Aplicando la fuerza de Lorentz directamente.
2.Mediante la regla de la mano derecha.
Los vectores 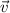 y
y 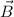 tienen por módulo 10 m/s y 15 T, respectivamente. Sus direcciones y sentidos son los indicados en la figura 1. Halla la fuerza de Lorentz que sufre una carga de 2C que se mueve a la velocidad
tienen por módulo 10 m/s y 15 T, respectivamente. Sus direcciones y sentidos son los indicados en la figura 1. Halla la fuerza de Lorentz que sufre una carga de 2C que se mueve a la velocidad 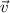 en el seno de un campo magnético
en el seno de un campo magnético 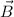 .
.
Un protón penetra en una región donde existe un campo magnético uniforme. Explique qué tipo de trayectoria describirá el protón si su velocidad es: a) paralela al campo; b) perpendicular al campo.
1.¿Qué sucede si el protón se abandona en reposo en el campo magnético?
2.¿En qué cambiarían las anteriores respuestas si en lugar de un protón fuera un electrón?
Un electrón se mueve con una velocidad de 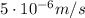 . Con una dirección ortogonal a su velocidad actúa un campo magnético de módulo 10T. Calcula:
. Con una dirección ortogonal a su velocidad actúa un campo magnético de módulo 10T. Calcula:
1.Fuerza que experimenta el electrón a causa del campo magnético.
2.Radio de la curvatura de su trayectoria.
3.Tiempo que tarda el electrón en describir una circunferencia completa.
Datos: 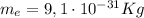 ,
, 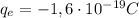 .
.
¿Con qué radio de curvatura se mueve una partícula con 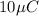 de carga y 0,5mg de masa cuando entra en una región con campo magnético de módulo 2T, perpendicularmente a las líneas de campo, y con una velocidad de 1000Km/s?
de carga y 0,5mg de masa cuando entra en una región con campo magnético de módulo 2T, perpendicularmente a las líneas de campo, y con una velocidad de 1000Km/s?
Tomamos los ejes coordenados de forma que el campo magnético va según el eje OZ, 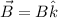 . Según el enunciado, la velocidad es perpendicular al campo magnético, ésta debe estar en el plano OXY, es decir
. Según el enunciado, la velocidad es perpendicular al campo magnético, ésta debe estar en el plano OXY, es decir 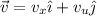 . Para obtener la fuerza magnética total, debemos efectuar el producto vectorial de ambas cantidades, en virtud de la fuerza de Lorentz,
. Para obtener la fuerza magnética total, debemos efectuar el producto vectorial de ambas cantidades, en virtud de la fuerza de Lorentz,
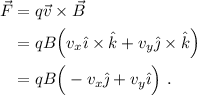
Según la segunda ley de Newton, esta fuerza debe ser igual a la masa por la aceleración, 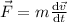 . Esto nos da dos ecuaciones diferenciales acopladas,
. Esto nos da dos ecuaciones diferenciales acopladas,
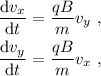
Para resolver este sistema, derivamos respecto al tiempo la primera de las ecuaciones en (2),
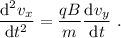
Podemos simplificar el sistema substituyendo las derivadas primeras en (3) según su valor obtenido de (2),
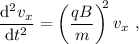
que es la ecuación de un oscilador armónico, cuya solución general es
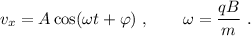
Integrando una vez este resultado, tenemos
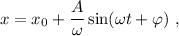
donde 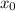 es una constante de integración. Por otra parte,
es una constante de integración. Por otra parte, 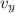 se obtiene directamente (2),
se obtiene directamente (2),
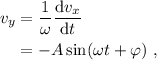
que integrando nos da la coordenada y,
donde 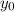 es otra constante de integración (que no tiene por que ser el valor inicial de la coordenada).
es otra constante de integración (que no tiene por que ser el valor inicial de la coordenada).
Como condiciones iniciales, imponemos que la velocidad en el instante inicial es paralela al eje OX, 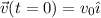 . Substituyendo en (5) y (7), obtenemos
. Substituyendo en (5) y (7), obtenemos

En resumen, la trayectoria de la partícula es
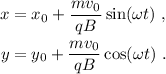
Podemos ver que el movimiento de la partícula es la composición de dos movimientos armónicos, de igual frecuencia y amplitud, en las dos direcciones coordenadas. El resultado de esta composición de movimientos armónicos es un movimiento circular uniforme. Podemos comprobarlo elevando al cuadrado la ecuación (10),
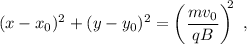
que, en efecto, es la ecuación de una trayectoria circular de radio
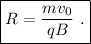
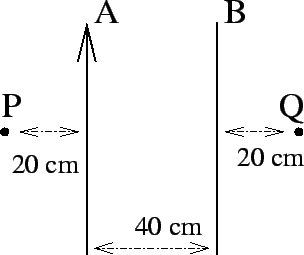
En la figura se representan dos hilos conductores de longitud indefinida. Por A circula una intensidad de 12A.
1.Calcula el valor y sentido de la intensidad que circula por B, teniendo en cuenta que el campo magnético en el punto Q es nulo.
2.¿Cuál es el valor, dirección y sentido del campo magnético en el punto P?
3.¿Qué fuerza, en función de la longitud de los cables (que es la misma), se ejercen los hilos entre sí? ¿Se atraen o se repelen?
Determina la fuerza que ejerce un hilo conductor recto de 5m de longitud, por el que circula una corriente de 5A, sobre otro hilo paralelo y igual al primero, separado 10cm de éste, por el que circula una corriente de 10A en el mismo sentido.
Una esfera sólida de masa  gira uniformemente alrededor de su eje con una carga
gira uniformemente alrededor de su eje con una carga 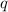 distribuida uniformemente en su superficie. Probar que el momento magnético
distribuida uniformemente en su superficie. Probar que el momento magnético 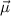 esta relacionado con el momento angular
esta relacionado con el momento angular 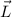 , por:
, por:
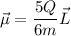
Un disco de radio  lleva una carga fija de densidad
lleva una carga fija de densidad 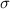 y gira con una velocidad angular
y gira con una velocidad angular 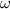 .
.
1.Halle la inducción magnética 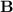 en un punto situado en el eje de simetría del disco a una distancia
en un punto situado en el eje de simetría del disco a una distancia  del centro.
del centro.
2.Halle la inducción magnética 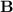 en el centro del disco.
en el centro del disco.
1.Un disco no conductor de pequeño grosor de masa  , uniformenente distribuida en toda la superficie del mismo, y radio
, uniformenente distribuida en toda la superficie del mismo, y radio  posee una densidad superficial de carga uniforme
posee una densidad superficial de carga uniforme 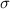 y gira con velocidad angular
y gira con velocidad angular 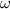 alrededor de su eje. Determine el momento (dipolar) magnético del disco en rotación.
alrededor de su eje. Determine el momento (dipolar) magnético del disco en rotación.
2.Una esfera sólida de radio  posee una densidad de carga uniforme
posee una densidad de carga uniforme 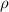 y una carga total
y una carga total 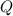 . La esfera gira alrededor de su diámetro con velocidad angular
. La esfera gira alrededor de su diámetro con velocidad angular 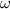 , y posee una masa total
, y posee una masa total  uniformenente distribuida en toda ella. Con la ayuda del resultado del apartado anterior, calcule el momento (dipolar) magnético de la esfera giratoria.
uniformenente distribuida en toda ella. Con la ayuda del resultado del apartado anterior, calcule el momento (dipolar) magnético de la esfera giratoria.
3.Para la esfera sólida, demuestre que los vectores de momento magnético y momento angular están relacionados por 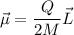 , resultado de validez general para cuerpos con densidades de carga y masa ambas uniformes, con
, resultado de validez general para cuerpos con densidades de carga y masa ambas uniformes, con 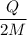 el denominado factor giromagnético.
el denominado factor giromagnético.
En módulo, se tiene que
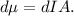
La carga diferencial de cada espira infinitesimal de radio  del disco giratorio será
del disco giratorio será
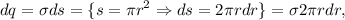
y de esta manera
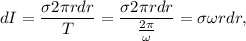
además
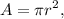
con lo que
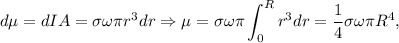
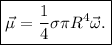
Podemos considerar que la esfera sólida giratoria está dividida en discos giratorios infinitesimales. Para encontrar el momento dipolar magnético de cada uno de estos discos giratorios, podemos usar el resultado del apartado anterior, si hacemos 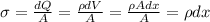 , donde
, donde 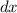 es el grosor infinitesimal de cada disco. Por otra parte el radio al cuadrado de cada disco infinitesimal varía de la siguiente manera, en función de
es el grosor infinitesimal de cada disco. Por otra parte el radio al cuadrado de cada disco infinitesimal varía de la siguiente manera, en función de  :
:  con
con  el radio de la esfera (aplíquese el Teorema de Pitágoras), luego
el radio de la esfera (aplíquese el Teorema de Pitágoras), luego
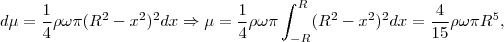
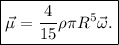
Empezamos expresando el momento magnético de la esfera en función de la carga
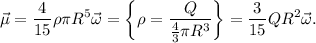
También se tiene que 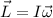 donde
donde 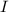 es el momento de inercia de la esfera sólida con respecto al eje de rotación (un diámetro del mismo en este caso),
es el momento de inercia de la esfera sólida con respecto al eje de rotación (un diámetro del mismo en este caso), 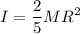 . Se tiene que
. Se tiene que 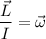 , que sustituyendo en la expresión de
, que sustituyendo en la expresión de 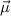 da
da
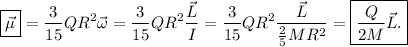
Este problema ha puesto de manifiesto que es posible obtener el momento dipolar magnético de un objeto que tiene su carga y masa distribuidas de forma uniforme (y de la misma manera - a una distribución volumétrica de carga le debe corresponder una volumétrica de masa) conociendo el momento de inercia en torno al eje de giro y el factor giromagnético 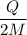 , ya que
, ya que
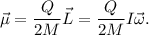



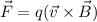 . Esta fuerza es central, ya que siempre es perpendicular a la velocidad. Por tanto, podemos igualar, su módulos con la fuerza centrípeta:
. Esta fuerza es central, ya que siempre es perpendicular a la velocidad. Por tanto, podemos igualar, su módulos con la fuerza centrípeta: